![[Previous]](../prev.gif) |
![[Contents]](../contents.gif) |
![[Index]](../keyword_index.gif) |
![[Next]](../next.gif) |
![[Previous]](../prev.gif) |
![[Contents]](../contents.gif) |
![[Index]](../keyword_index.gif) |
![[Next]](../next.gif) |
Log gamma function
#include <math.h>
double gamma( double x );
double gamma_r( double x,
int* signgam);
float gammaf( float x );
float gammaf_r( float x,
int* signgam);
libm
Use the -l m option to qcc to link against this library.
The gamma() and gamma_r() functions return the natural log (ln) of the gamma() function and are equivalent to lgamma(). These functions return ln|Γ(x)|, where Γ(x) is defined as follows:
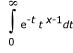
The results converge when x is between 0 and 1. The Γ function has the property:
Γ(N) = Γ(N-1)×N
The gamma* functions compute the log because the Γ function grows very quickly.
The gamma() and gammaf() functions use the external integer signgam to return the sign of Γ(x), while gamma_r() and gammaf_r() use the user-allocated space addressed by signgamp.
 |
The signgam variable isn't set until gamma() or
gammaf() returns.
For example, don't use the expression:
g = signgam * exp( gamma( x )); to compute g = Γ(x)'. Instead, compute gamma() first: lg = gamma(x); g = signgam * exp( lg ); |
Note that Γ(x) must overflow when x is large enough, underflow when -x is large enough, and generate a division by 0 exception at the singularities x a nonpositive integer.
ln|Γ(x)|
 |
If an error occurs, these functions return 0, but this is also a valid mathematical result. If you want to check for errors, set errno to 0, call the function, and then check errno again. These functions don't change errno if no errors occurred. |
| Safety: | |
|---|---|
| Cancellation point | No |
| Interrupt handler | No |
| Signal handler | No |
| Thread | Yes |
![[Previous]](../prev.gif) |
![[Contents]](../contents.gif) |
![[Index]](../keyword_index.gif) |
![[Next]](../next.gif) |