Log gamma function
Synopsis:
#include <math.h>
double lgamma( double x );
double lgamma_r( double x,
int* signgamp );
float lgammaf( float x );
float lgammaf_r( float x,
int* signgamp );
long double lgammal( long double x );
long double lgammal_r( long double x,
int* signgamp );
extern int signgam;
Arguments:
- x
- An arbitrary number.
- signgamp
- (lgamma_r(), lgammaf_r(), and lgammal_r() only) A pointer to a location where the function can store the sign of Γ(x).
Library:
- libm
- The general-purpose math library.
- libm-sve
- (QNX Neutrino 7.1 or later) A library that optimizes the code for ARMv8.2 chips that have Scalable Vector Extension hardware.
Your system requirements will determine how you should work with these libraries:
- If you want only selected processes to run with the SVE version, you can include both libraries in your OS image and use the -l m or -l m-sve option to qcc to link explicitly against the appropriate one.
- If you want all processes to use the SVE version, include libm-sve.so in your OS image and set up a symbolic link from libm.so to libm-sve.so. Use the -l m option to qcc to link against the library.
Description:
The lgamma*() and lgamma*_r() functions return the natural log (ln) of the Γ function. These functions return ln|Γ(x)|, where Γ(x) is defined as follows:
- For x > 0.0:
-
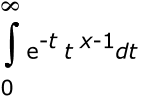
- For x < 1.0:
- n / (Γ( 1-x ) * sin( nx ))
Γ(N) = Γ(N-1)×N
The lgamma* functions compute the log because the Γ function grows very quickly.
The lgamma() and lgammaf() functions use the external integer signgam to return the sign of Γ(x), while lgamma_r() and lgammaf_r() use the user-allocated space addressed by signgamp.
g = signgam * exp( lgamma( x ));to compute g = Γ(x)'. Instead, compute lgamma() first:
lg = lgamma(x); g = signgam * exp( lg );
Note that Γ(x) must overflow when x is large enough, underflow when -x is large enough, and generate a division by 0 exception at the singularities x a nonpositive integer.
To check for error situations, use feclearexcept() and fetestexcept(). For example:
- Call feclearexcept(FE_ALL_EXCEPT) before calling lgamma(), lgamma_r(), lgammaf(), lgammaf_r(), lgammal(), or lgammal_r().
- On return, if fetestexcept(FE_ALL_EXCEPT) is nonzero, then an error has occurred.
Returns:
ln|Γ(x)|
| If: | These functions return: | Errors: |
|---|---|---|
| x is 1.0 or 2.0 | 0.0 | — |
| x is a non-positive integer | Inf | FE_DIVBYZERO |
| x is ±Inf | Inf | — |
| x is NaN | NaN | — |
| The correct value would cause overflow | Inf | FE_OVERFLOW |
These functions raise FE_INEXACT if the FPU reports that the result can't be exactly represented as a floating-point number.
Examples:
#include <stdio.h>
#include <fenv.h>
#include <inttypes.h>
#include <math.h>
#include <stdlib.h>
int main(int argc, char** argv)
{
double a, b;
int except_flags;
a = 0.5;
feclearexcept(FE_ALL_EXCEPT);
b = lgamma(a);
except_flags = fetestexcept(FE_ALL_EXCEPT);
if(except_flags) {
/* An error occurred; handle it appropriately. */
}
printf("lgamma(%f) = %f \n", a, b);
return EXIT_SUCCESS;
}
produces the output:
lgamma(0.500000) = 0.572365 0
Classification:
lgamma(), lgammaf(), and lgammal() are C11, POSIX 1003.1; lgamma_r(), lgammaf_r(), and lgammal_r() are QNX Neutrino
| Safety: | |
|---|---|
| Cancellation point | No |
| Interrupt handler | Yes |
| Signal handler | Yes |
| Thread | Yes |