When one module depends on another module, we say that the modules are connected in series—the failure of one module results in a failure of the system:
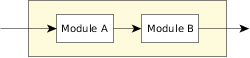 Figure 1. Aggregate module formed by two modules in series.
Figure 1. Aggregate module formed by two modules in series.If module A has an availability of Xa, and module B has an availability of Xb, the combined availability of a subsystem constructed of modules A and B connected in series is:
availability = Xa × Xb
Practically speaking, if both modules have a five nines availability, the system constructed from connecting the two modules in series will be 99.998%:
availability = 0.99999 * 0.99999
= 0.99998
You need to be careful here, because the numbers don't look too bad, after all, the difference between 0.99999 and 0.99998 is only 0.00001—hardly worth talking about, right? Well, that's not the case—the system now has double the amount of downtime! Let's do the math.
Suppose we wish to see how much downtime we'll have during a year. One year has 365 × 24 × 60 × 60 seconds (31 and a half million seconds). If we have an availability of five nines, it means that we have an unavailability factor of 0.00001 (1 minus 0.99999)
Therefore, taking the 31 and a half million seconds times 0.00001 gives us 315 seconds, or just over five minutes of downtime per year. If we use our new serial availability, 0.99998, and multiply the unavailability (1 minus 0.99998, or 0.00002), we come up with 630 seconds, or 10.5 minutes of downtime—double the amount of downtime!
The reason the math is counter-intuitive is because in order to calculate downtime, we're using the unavailability number (that is, one minus the availability number).