<random>[added with C++11]
bernoulli_distribution
· binomial_distribution
· discard_block
· exponential_distribution
· gamma_distribution
· geometric_distribution
· linear_congruential
· mersenne_twister
· minstd_rand0
· minstd_rand
· mt19937
· normal_distribution
· operator!=
· operator==
· operator<<
· operator>>
· poisson_distribution
· random_device
· ranlux_base_01
· ranlux3
· ranlux3_01
· ranlux4
· ranlux4_01
· ranlux64_base_01
· subtract_with_carry
· subtract_with_carry_01
· uniform_int
· uniform_real
· variate_generator
· xor_combine
cauchy_distribution
· chi_squared_distribution
· default_random_engine
· discard_block_engine
· discrete_distribution
· extreme_value_distribution
· fisher_f_distribution
· generate_canonical
· independent_bits_engine
· knuth_b
· linear_congruential_engine
· lognormal_distribution
· mersenne_twister_engine
· mt19937_64
· negative_binomial_distribution
· piecewise_constant_distribution
· piecewise_linear_distribution
· ranlux24
· ranlux24_base
· ranlux48
· ranlux48_base
· seed_seq
· shuffle_order_engine
· student_t_distribution
· subtract_with_carry_engine
· uniform_int_distribution
· uniform_real_distribution
· weibull_distribution
Include the TR1
header <random> to define a host of
random number generators.
For an overview of concepts related to this header, see
Random Number Generators.
namespace std {
// UTILITIES
template<class RealType,
size_t bits,
class Engine>
RealType generate_canonical(Engine& gen); [added with C++11]
class seed_seq; [added with C++11]
template<class Engine,
class Dist>
class variate_generator; [removed with C++11]
// SIMPLE ENGINES
template<class UIntType,
UIntType A, UIntType C, UIntType M>
class linear_congruential;
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
class mersenne_twister;
template<class IntType,
IntType M, int S, int R>
class subtract_with_carry;
template<class RealType,
int W, int S, int R>
class subtract_with_carry_01;
class random_device;
template<class UIntType,
UIntType A, UIntType C, UIntType M>
class linear_congruential_engine; [added with C++11]
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U,
UIntType D, int S,
UIntType B, int T,
UIntType C, int L,
UIntType F>
class mersenne_twister_engine; [added with C++11]
template<class IntType,
int W, int S, int R>
class subtract_with_carry_engine; [added with C++11]
// COMPOUND ENGINES
template<class Engine,
int P, int R>
class discard_block;
template<class Engine1, int S1,
class Engine2, int S2>
class xor_combine;
template<class Engine,
size_t P, size_t R>
class discard_block_engine; [added with C++11]
template<class Engine,
size_t W, class UIntType>
class independent_bits_engine; [added with C++11]
template<class Engine,
size_t K>
class shuffle_order_engine; [added with C++11]
// ENGINES WITH PREDEFINED PARAMETERS
typedef linear_congruential_engine<ui-type, 16807, 0, 2147483647> minstd_rand0;
typedef linear_congruential_engine<ui-type, 48271, 0, 2147483647> minstd_rand;
typedef mersenne_twister<ui-type, 32, 624, 397, 31,
0x9908b0df, 11, 7, 0x9d2c5680, 15, 0xefc60000, 18> mt19937;
typedef mersenne_twister_engine<ui-type, 64, 312, 156, 31,
0xb5026f5aa96619e9ULL, 29, 0x5555555555555555ULL, 17,
0x71d67fffeda60000ULL, 37, 0x0ff7eee000000000ULL, 43,
6364136223846793005ULL> mt19937_64 [added with C++11];
typedef subtract_with_carry_01<float, 24, 10, 24> ranlux_base_01;
typedef subtract_with_carry_01<double, 48, 10, 24> ranlux64_base_01;
typedef discard_block<subtract_with_carry<ui-type, 1 << 24, 10, 24>,
223, 24> ranlux3;
typedef discard_block<subtract_with_carry<ui-type, 1 << 24, 10, 24>,
389, 24> ranlux4;
typedef discard_block<ranlux_base_01, 223, 24> ranlux3_01;
typedef discard_block<ranlux_base_01, 389, 24> ranlux4_01;
typedef shuffle_order_engine<minstd_rand0, 256>
knuth_b; [added with C++11]
typedef subtract_with_carry_engine<ui-type, 24, 10, 24>
ranlux24_base; [added with C++11]
typedef discard_block_engine<ranlux_24_base, 223, 23>
ranlux24; [added with C++11]
typedef subtract_with_carry_engine<ui-type, 48, 5, 12>
ranlux48_base; [added with C++11]
typedef discard_block_engine<ranlux_48_base, 389, 11>
ranlux48; [added with C++11]
typedef Rand default_random_engine; [added with C++11]
// DISTRIBUTIONS
template<class RealType = double>
class bernoulli_distribution;
template<class IntType = int, class RealType = double>
class binomial_distribution;
template<class IntType = int, class RealType = double>
class geometric_distribution;
template<class IntType = int, class RealType = double>
class poisson_distribution;
template<class IntType = int>
class uniform_int;
template<class RealType = double>
class exponential_distribution;
template<class RealType = double>
class gamma_distribution;
template<class RealType = double>
class normal_distribution;
template<class RealType = double>
class uniform_real;
template<class IntType = int>
class discrete_distribution; [added with C++11]
template<class IntType = int>
class negative_binomial_distribution; [added with C++11]
template<class IntType = int>
class uniform_int_distribution; [added with C++11]
template<class RealType = double>
class cauchy_distribution; [added with C++11]
template<class RealType = double>
class chi_squared_distribution; [added with C++11]
template<class RealType = double>
class extreme_value_distribution; [added with C++11]
template<class RealType = double>
class fisher_f_distribution; [added with C++11]
template<class RealType = double>
class lognormal_distribution; [added with C++11]
template<class RealType = double>
class piecewise_constant_distribution; [added with C++11]
template<class RealType = double>
class piecewise_linear_distribution; [added with C++11]
template<class RealType = double>
class student_t_distribution; [added with C++11]
template<class RealType = double>
class uniform_real_distribution; [added with C++11]
template<class RealType = double>
class weibull_distribution; [added with C++11]
// OPERATORS
template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator==(
const linear_congruential<UIntType, A, C, M>& left,
const linear_congruential<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator==(
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& left,
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class IntType,
IntType M, int S, int R>
bool operator==(
const subtract_with_carry<IntType, M, S, R>& left,
const subtract_with_carry<IntType, M, S, R>& right);
template<class RealType,
int W, int S, int R>
bool operator==(
const subtract_with_carry_01<RealType, W, S, R>& left,
const subtract_with_carry_01<RealType, W, S, R>& right);
template<class Engine,
int P, int R>
bool operator==(
const discard_block<Engine, F, R>& left,
const discard_block<Engine, F, R>& right);
template<class Engine1, int S1,
class Engine2, int S2>
bool operator==(
const xor_combine<Engine1, S1, Engine2, S2>& left,
const xor_combine<Engine1, S1, Engine2, S2>& right);
template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator==( [added with C++11]
const linear_congruential_engine<UIntType, A, C, M>& left,
const linear_congruential_engine<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator==( [added with C++11]
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& left,
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class IntType,
IntType M, int S, int R>
bool operator==( [added with C++11]
const subtract_with_carry_engine<IntType, A, C, M>& left,
const subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Engine,
size_t P, size_t R>
bool operator==( [added with C++11]
const discard_block_engine<Engine, F, R>& left,
const discard_block_engine<Engine, F, R>& right);
template<class Engine,
size_t W, class UIntType>
bool operator==( [added with C++11]
const independent_bits_engine<Engine, W, U>& left,
const independent_bits_engine<Engine, W, U>& right);
template<class Engine,
size_t K>
bool operator==( [added with C++11]
const ahuffle_order_engine<Engine, K>& left,
const shuffle_order_engine<Engine, K>& right);
template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator!=(
const linear_congruential<UIntType, A, C, M>& left,
const linear_congruential<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator!=(
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& left,
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class IntType,
IntType M, int S, int R>
bool operator!=(
const subtract_with_carry<IntType, M, S, R>& left,
const subtract_with_carry<IntType, M, S, R>& right);
template<class RealType,
int W, int S, int R>
bool operator!=(
const subtract_with_carry_01<RealType, W, S, R>& left,
const subtract_with_carry_01<RealType, W, S, R>& right);
template<class Engine,
int P, int R>
bool operator!=(
const discard_block<Engine, F, R>& left,
const discard_block<Engine, F, R>& right);
template<class Engine1, int S1,
class Engine2, int S2>
bool operator!=(
const xor_combine<Engine1, S1, Engine2, S2>& left,
const xor_combine<Engine1, S1, Engine2, S2>& right);
template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator!=( [added with C++11]
const linear_congruential_engine<UIntType, A, C, M>& left,
const linear_congruential_engine<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator!=( [added with C++11]
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& left,
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class IntType,
IntType M, int S, int R>
bool operator!=( [added with C++11]
const subtract_with_carry_engine<IntType, A, C, M>& left,
const subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Engine,
size_t P, size_t R>
bool operator!=( [added with C++11]
const discard_block_engine<Engine, F, R>& left,
const discard_block_engine<Engine, F, R>& right);
template<class Engine,
size_t W, class UIntType>
bool operator!=( [added with C++11]
const independent_bits_engine<Engine, W, U>& left,
const independent_bits_engine<Engine, W, U>& right);
template<class Engine,
size_t K>
bool operator!=( [added with C++11]
const ahuffle_order_engine<Engine, K>& left,
const shuffle_order_engine<Engine, K>& right);
template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const linear_congruential<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const subtract_with_carry<IntType, M, S, R>& right);
template<class Elem, class Traits, class RealType,
int W, int S, int R>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const subtract_with_carry_01<RealType, W, S, R>& right);
template<class Elem, class Traits, class Engine,
int P, int R>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const discard_block<Engine, F, R>& right);
template<class Elem, class Traits, class Engine1, int S1,
class Engine2, int S2>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const xor_combine<Engine1, S1, Engine2, S2>& right);
template<class Elem, class Traits>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const bernoulli_distribution& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const binomial_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const exponential_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const gamma_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const geometric_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const normal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const poisson_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const uniform_int<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const uniform_real<RealType>& right);
template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const linear_congruential_engine<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Elem, class Traits, class Engine,
size_t P, size_t R>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const discard_block_engine<Engine, F, R>& right);
template<class Elem, class Traits, class Engine,
size_t W, class UIntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const independent_bits_engine<Engine, W, U>& right);
template<class Elem, class Traits, class Engine,
size_t K>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const shuffle_order_engine<Engine, K>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const cauchy_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const chi_squared_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const discrete_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const extreme_value_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const fisher_f_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const lognormal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const negative_binomial_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const piecewise_constant_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const student_t_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const uniform_int_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const uniform_real_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const weibull_distribution<RealType>& right);
template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
linear_congruential<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
subtract_with_carry<IntType, M, S, R>& right);
template<class Elem, class Traits, class RealType,
int W, int S, int R>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
subtract_with_carry_01<RealType, W, S, R>& right);
template<class Elem, class Traits, class Engine,
int P, int R>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
discard_block<Engine, F, R>& right);
template<class Elem, class Traits, class Engine1, int S1,
class Engine2, int S2>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
xor_combine<Engine1, S1, Engine2, S2>& right);
template<class Elem, class Traits>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
bernoulli_distribution& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
binomial_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
exponential_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
gamma_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
geometric_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
normal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
poisson_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
uniform_int<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
uniform_real<RealType>& right);
template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
linear_congruential_engine<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, R>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Elem, class Traits, class Engine,
size_t P, size_t R>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
discard_block_engine<Engine, F, R>& right);
template<class Elem, class Traits, class Engine,
size_t W, class UIntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
independent_bits_engine<Engine, W, U>& right);
template<class Elem, class Traits, class Engine,
size_t K>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
shuffle_order_engine<Engine, K>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
cauchy_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
chi_squared_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
discrete_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
extreme_value_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
fisher_f_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
lognormal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
negative_binomial_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
piecewise_constant_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
student_t_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
uniform_int_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
uniform_real_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
weibull_distribution<RealType>& right);
namespace tr1 {
using std::bernoulli_distribution; [added with C++11]
using std::binomial_distribution;
using std::discard_block; using std::exponential_distribution;
using std::gamma_distribution; using std::geometric_distribution;
using std::linear_congruential; using std::mersenne_twister;
using std::minstd_rand; using std::minstd_rand0;
using std::mt19937; using std::normal_distribution;
using std::poisson_distribution; using std::random_device;
using std::ranlux4; using std::ranlux3;
using std::ranlux3_01; using std::ranlux4;
using std::ranlux4_01; using std::ranlux64_base_01;
using std::ranlux_base_01; using std::subtract_with_carry;
using std::subtract_with_carry_01; using std::uniform_int;
using std::uniform_real; using std::variate_generator;
using std::xor_combine;
using std::cauchy_distribution; using std::chi_squared_distribution;
using std::discard_block_engine; using std::discrete_distribution;
using std::extreme_value_distribution; using std::fisher_f_distribution;
using std::generate_canonical;
using std::knuth_b; using std::independent_bits_engine;
using std::linear_congruential_engine; using std::lognormal_distribution;
using std::mersenne_twister_engine; using std::mt19937_64;
using std::negative_binomial_distribution;
using std::piecewise_constant_distribution; piecewise_linear_distribution;
using std::ranlux24; using std::ranlux24_base; using std::ranlux48;
using std::ranlux48_base; using std::seed_seq;
using std::shuffle_order_engine; using std::student_t_distribution;
using std::subtract_with_carry_engine;
using std::uniform_int_distribution; using std::uniform_real_distribution;
using std::weibull_distribution;
} // namespace tr1
} // namespace std
bernoulli_distributionclass bernoulli_distribution {
public:
typedef int input_type; [removed with C++11]
struct param_type; [added with C++11]
explicit bernoulli_distribution(double p0 = 0.5);
explicit bernoulli_distribution(const param_type& par0); [added with C++11]
double p() const;
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const; [added with C++11]
result_type max() const; [added with C++11]
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
double stored_p; // exposition only
};
The class describes a distribution
that produces values of type bool, returning true with a
probability given by the argument to the constructor.
bernoulli_distribution::bernoulli_distributionexplicit bernoulli_distribution(double p0 = 0.5); explicit bernoulli_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 <= p0 && p0 <= 1.0
The first constructor constructs an object whose stored value stored_p
holds the value p0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
bernoulli_distribution::input_typetypedef int input_type; [removed with C++11]
The type is a synonym for int.
bernoulli_distribution::maxresult_type max() const; [added with C++11]
The member function returns true.
bernoulli_distribution::minresult_type min() const; [added with C++11]
The member function returns false.
bernoulli_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member operator uses the engine eng
as a source of uniformly distributed random integer values and returns true
with probability given by the stored value stored_p.
The second member function behaves the same, except that it uses the parameters
stored in par0.
bernoulli_distribution::pdouble p() const;
The member function returns the stored value stored_p.
bernoulli_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
bernoulli_distribution::param_typestruct param_type { [added with C++11]
typedef bernoulli_distribution distribution_type;
param_type(double p0 = 0.5);
double p() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
bernoulli_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
bernoulli_distribution::result_typetypedef bool result_type;
The type is a synonym for bool.
binomial_distributiontemplate<class IntType = int,
class RealType = double> [always double with C++11]
class binomial_distribution {
public:
typedef T1 input_type; [removed with C++11]
typedef IntType result_type;
struct param_type; [added with C++11]
explicit binomial_distribution(result_type t0 = 1,
RealType p0 = RealType(0.5));
explicit binomial_distribution(const param_type& par0); [added with C++11]
result_type t() const;
RealType p() const;
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const; [added with C++11]
result_type max() const; [added with C++11]
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
result_type stored_t; // exposition only
RealType stored_p; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type distributed with a binomial distribution.
binomial_distribution::binomial_distributionbinomial_distribution(result_type t0 = 1,
RealType p0 = RealType(0.5));
explicit binomial_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 <= t0 && 0.0 <= p0 && p0 <= 1.0
The first constructor constructs an object whose stored value stored_p
holds the value p0 and whose stored value stored_t holds
the value t0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
binomial_distribution::input_typetypedef T1 input_type; [removed with C++11]
The type is a synonym for the implementation-defined type T1.
binomial_distribution::maxresult_type max() const; [added with C++11]
The member function returns the largest value returnable by
operator().
binomial_distribution::minresult_type min() const; [added with C++11]
The member function returns the smallest value returnable by
operator().
binomial_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
integral values with each value i occurring with probability:
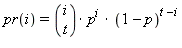
The second member function behaves the same, except that it uses the parameters
stored in par0.
binomial_distribution::pRealType p() const;
The member function returns the stored value stored_p.
binomial_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
binomial_distribution::param_typestruct param_type { [added with C++11]
typedef binomial_distribution<IntType, RealType> distribution_type;
param_type(result_type t0 = 1, RealType p0 = RealType(0.5));
result_type t() const;
RealType p() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
binomial_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
binomial_distribution::result_typetypedef IntType result_type;
The type is a synonym for IntType.
binomial_distribution::tresult_type t() const;
The member function returns the stored value stored_t.
cauchy_distributiontemplate<class RealType = double>
class cauchy_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit cauchy_distribution(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
explicit cauchy_distribution(const param_type& par0);
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_a; // exposition only
result_type stored_b; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with a Cauchy distribution.
cauchy_distribution::aresult_type a() const;
The member function returns the stored value stored_a.
cauchy_distribution::bresult_type b() const;
The member function returns the stored value stored_b.
cauchy_distribution::cauchy_distributioncauchy_distribution(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
explicit cauchy_distribution(const param_type& par0);
Precondition: 0.0 < b0
The first constructor constructs an object whose stored value stored_a
holds the value a0 and whose stored value stored_b holds
the value b0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
cauchy_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
cauchy_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
cauchy_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
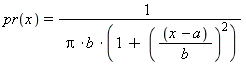
The second member function behaves the same, except that it uses the parameters
stored in par0.
cauchy_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
cauchy_distribution::param_typestruct param_type {
typedef cauchy_distribution<RealType> distribution_type;
param_type(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
result_type a() const;
result_type b() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
cauchy_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
cauchy_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
chi_squared_distributiontemplate<class RealType = double>
class chi_squared_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit chi_squared_distribution(RealType n0 = 1);
explicit chi_squared_distribution(const param_type& par0);
RealType n() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
RealType stored_n; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with a chi-squared distribution.
chi_squared_distribution::chi_squared_distributionchi_squared_distribution(RealType n0 = 1); explicit chi_squared_distribution(const param_type& par0);
Precondition: 0.0 < n0
The first constructor constructs an object whose stored value stored_n
holds the value n0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
chi_squared_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
chi_squared_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
chi_squared_distribution::nRealType n() const;
The member function returns the stored value stored_n.
chi_squared_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
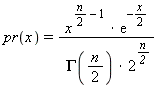
The second member function behaves the same, except that it uses the parameters
stored in par0.
chi_squared_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
chi_squared_distribution::param_typestruct param_type {
typedef chi_squared_distribution<RealType> distribution_type;
param_type(int n0 = 1);
RealType n() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
chi_squared_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
chi_squared_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
default_random_enginetypedef Rand default_random_engine; [added with C++11]
The type is a synonym for Rand, a predefined
engine.
discard_blocktemplate<class Engine,
int P, int R>
class discard_block {
public:
typedef Engine base_type;
typedef typename base_type::result_type result_type;
static constexpr int block_size = P;
static constexpr int used_block = R;
discard_block();
explicit discard_block(const base_type& eng);
explicit discard_block(base_type&& eng);
template<class Gen>
discard_block(Gen& gen);
void seed();
template<class Gen>
void seed(Gen& gen);
const base_type& base() const;
result_type min() const;
result_type max() const;
result_type operator()();
private:
Engine stored_eng; // exposition only
int count; // exposition only
};
The template class describes a compound engine
that produces values by discarding some of the values returned by its base engine. Each
cycle of the compound engine begins by returning R values successively produced
by the base engine and ends by discarding P - R such values.
The engine's state is the state of stored_eng
followed by the number of calls to operator() that have occurred since the
beginning of the current cycle.
The value of the template argument R must be less than or
equal to the value of the template argument P.
discard_block::baseconst base_type& base() const;
The member function returns a reference to the underlying engine object.
discard_block::base_typetypedef Engine base_type;
The type is a synonym for the type of the underlying engine object.
discard_block::block_sizestatic constexpr int block_size = P;
The static const variable holds the value of the template argument P, the number
of values in each cycle.
discard_block::discard_blockdiscard_block();
explicit discard_block(const base_type& eng);
explicit discard_block(base_type&& eng);
template<class Gen>
discard_block(Gen& gen);
The first constructor constructs a discard_block object with a default-initialized
engine. The second contructor constructs a discard_block object with a copy of an
engine object. The third contructor constructs a discard_block object by moving the
engine object. The fourth constructor constructs a discard_block object with an engine
initialized from a generator.
discard_block::maxresult_type max() const;
The member function returns stored_eng.max().
discard_block::minresult_type min() const;
The member function returns stored_eng.min().
discard_block::operator()result_type operator()();
The member function returns the next value in the sequence.
discard_block::result_typetypedef typename base_type::result_type result_type;
The type is a synonym for base_type::result_type.
discard_block::seedvoid seed();
template<class Gen>
void seed(Gen& gen);
The first seed function
calls stored_eng.seed() and sets count to 0.
The second seed function calls stored_eng.seed(gen)
and sets count to 0.
discard_block::used_blockstatic constexpr int used_block = R;
The static const variable holds the value of the template argument R, the number
of values to return at the beginning of each cycle.
discard_block_enginetemplate<class Engine,
int P, int R>
class discard_block_engine { [added with C++11]
public:
typedef Engine base_type;
typedef typename base_type::result_type result_type;
static constexpr int block_size = P;
static constexpr int used_block = R;
discard_block_engine();
explicit discard_block_engine(const base_type& eng);
explicit discard_block_engine(result_type x0);
template<class Seed_seq>
explicit discard_block_engine(Seed_seq& seq);
void seed();
void seed(result_type x0);
template<class Seed_seq>
void seed(Seed_seq& seq);
const base_type& base() const noexcept;
static constexpr result_type min();
static constexpr result_type max();
result_type operator()();
void discard(unsigned long long count);
private:
Engine stored_eng; // exposition only
int count; // exposition only
};
The template class describes a compound engine
that produces values by discarding some of the values returned by its base engine. Each
cycle of the compound engine begins by returning R values successively produced
by the base engine and ends by discarding P - R such values.
The engine's state is the state of stored_eng
followed by the number of calls to operator() that have occurred since the
beginning of the current cycle.
The value of the template argument R must be less than or
equal to the value of the template argument P.
discard_block_engine::baseconst base_type& base() const noexcept;
The member function returns a reference to the underlying engine object.
discard_block_engine::base_typetypedef Engine base_type;
The type is a synonym for the type of the underlying engine object.
discard_block_engine::block_sizestatic constexpr int block_size = P;
The static const variable holds the value of the template argument P, the number
of values in each cycle.
discard_block_engine::discardvoid discard(unsigned long long count);
The member function effectively calls (*this)() count times.
discard_block_engine::discard_block_enginediscard_block_engine();
explicit discard_block_engine(const base_type& eng);
explicit discard_block_engine(result_type x0);
template<class Seed_seq>
explicit discard_block_engine(Seed_seq& seq);
The first constructor constructs a discard_block_engine object with a default-initialized
engine. The second contructor constructs a discard_block_engine object with a copy of an
engine object. The third constructor constructs a discard_block_engine object with its engine
initialized by stored_engine(x0).
The fourth constructor constructs a
discard_block_engine object with its engine initialized by
stored_engine(seq).
Unless Seed_seq is not convertible to result_type,
the fourth constructor does not participate in overload resolution.
discard_block_engine::_maxstatic constexpr result_type max();
The static member function returns Engine::max().
discard_block_engine::minstatic result_type min();
The static member function returns Engine::min().
discard_block_engine::operator()result_type operator()();
The member function returns the next value in the sequence.
discard_block_engine::result_typetypedef typename base_type::result_type result_type;
The type is a synonym for base_type::result_type.
discard_block_engine::seedvoid seed();
void seed(result_type x0);
template<class Seed_seq>
void seed(Seed_seq& seq);
The first seed function
calls stored_eng.seed() and sets count to 0.
The second seed function calls stored_eng.seed(x0)
and sets count to 0.
The third seed function calls stored_eng.seed(seq)
and sets count to 0.
Unless Seed_seq is not convertible to result_type,
the third function does not participate in overload resolution.
discard_block_engine::used_blockstatic constexpr int used_block = R;
The static const variable holds the value of the template argument R, the number
of values to return at the beginning of each cycle.
discrete_distributiontemplate<class IntType = int>
class discrete_distribution { [added with C++11]
public:
typedef IntType result_type;
struct param_type;
discrete_distribution();
discrete_distribution(initializer_list<double> init);
explicit discrete_distribution(const param_type& par0);
template<class Fn>
discrete_distribution(size_t count,
double low, double high, Fn func);
explicit discrete_distribution(const param_type& par0);
vector<double> probabilities() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
vector<double> stored_p; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type distributed according to a uniform-width histogram of probabilities.
Three distributions are very similar:
discrete_distribution
has uniform-width intervals with uniform probability in each interval.piecewise_constant_distribution
has varying-width intervals with uniform probability in each interval.piecewise_linear_distribution
has varying-width intervals with linearly varying probability over each interval.discrete_distribution::discrete_distributiondiscrete_distribution();
discrete_distribution(initializer_list<double> init);
template<class Fn>
discrete_distribution(size_t count,
double low, double high, Fn func);
explicit discrete_distribution(const param_type& par0);
Precondition: All elements in init
are nonnegative and at least one is nonzero.
The first constructor constructs an object whose stored value stored_p
has one element with value 1.
The second constructor constructs an object whose stored value stored_p
is initialized with the sequence [init.begin(), init.end()),
then normalized so that the sum of all elements is 1.
If the sequence is empty, stored_p has one element with
value 1.
The third constructor constructs an object whose stored value stored_p
is initialized with count elements. It divides the range high - low
into count uniform subranges, then stores in element I
the value func(x) for x in the middle of subrange I.
If count < 1, stored_p has one element with
value 1.
The fourth constructor constructs an object whose stored parameters
are initialized from par0.
discrete_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
discrete_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
discrete_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
integral values with each value i in the range [0, stored_p.size() - 1)
occurring with probability stored_p[i] and all other values of i
occurring with probability zero.
The second member function behaves the same, except that it uses the parameters
stored in par0.
discrete_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
discrete_distribution::param_typestruct param_type {
typedef discrete_distribution<IntType> distribution_type;
param_type();
param_type(initializer_list<double> init);
template<class Fn>
param_type(size_t count,
double low, double high, Fn func);
vector<double> probabilities() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
discrete_distribution::probabilitiesvector<double> probabilities() const;
The member function returns the stored value stored_p.
discrete_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
discrete_distribution::result_typetypedef IntType result_type;
The type is a synonym for IntType.
exponential_distributiontemplate<class RealType = double>
class exponential_distribution {
public:
typedef RealType input_type; [removed with C++11]
typedef RealType result_type;
struct param_type; [added with C++11]
explicit exponential_distribution(result_type lambda0 = result_type(1.0));
explicit exponential_distribution(const param_type& par0); [added with C++11]
result_type lambda() const;
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const; [added with C++11]
result_type max() const; [added with C++11]
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
result_type stored_lambda; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type with an exponential distribution.
exponential_distribution::exponential_distributionexponential_distribution(result_type lambda0 = result_type(1.0)); explicit exponential_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 < lambda0
The first constructor constructs an object whose stored value stored_lambda
holds the value lambda0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
exponential_distribution::input_typetypedef RealType input_type; [removed with C++11]
The type is a synonym for RealType.
exponential_distribution::lambdaresult_type lambda() const;
The member function returns the stored value stored_lambda.
exponential_distribution::maxresult_type max() const; [added with C++11]
The member function returns the largest value returnable by
operator().
exponential_distribution::minresult_type min() const; [added with C++11]
The member function returns the smallest value returnable by
operator().
exponential_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member function uses the engine eng
as a source of uniformly distributed random values and returns
floating-point values with each value x occurring with probability:
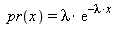
The second member function behaves the same, except that it uses the parameters
stored in par0.
exponential_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
exponential_distribution::param_typestruct param_type { [added with C++11]
typedef exponential_distribution<RealType> distribution_type;
param_type(result_type lambda0 = result_type(1.0));
result_type lambda() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
exponential_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
exponential_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
extreme_value_distributiontemplate<class RealType = double>
class extreme_value_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit extreme_value_distribution(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
explicit extreme_value_distribution(const param_type& par0);
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_a; // exposition only
result_type stored_b; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with an extreme-value (a.k.a. Gumbel Type I, log Weibull, or Fisher-Tippett Type I) distribution.
extreme_value_distribution::aresult_type a() const;
The member function returns the stored value stored_a.
extreme_value_distribution::bresult_type b() const;
The member function returns the stored value stored_b.
extreme_value_distribution::extreme_value_distributionextreme_value_distribution(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
explicit extreme_value_distribution(const param_type& par0);
Precondition: 0.0 < b0
The first constructor constructs an object whose stored value stored_a
holds the value a0 and whose stored value stored_b holds
the value b0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
extreme_value_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
extreme_value_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
extreme_value_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
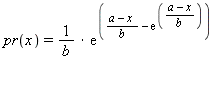
The second member function behaves the same, except that it uses the parameters
stored in par0.
extreme_value_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
extreme_value_distribution::param_typestruct param_type {
typedef extreme_value_distribution<RealType> distribution_type;
param_type(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
result_type a() const;
result_type b() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
extreme_value_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
extreme_value_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
fisher_f_distributiontemplate<class RealType = double>
class fisher_f_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit fisher_f_distribution(RealType m0 = 1,
RealType n0 = 1);
explicit fisher_f_distribution(const param_type& par0);
RealType m() const;
RealType n() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
RealType stored_m; // exposition only
RealType stored_n; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with a Fisher F distribution.
fisher_f_distribution::fisher_f_distributionfisher_f_distribution(RealType m0 = 1,
RealType n0 = 1);
explicit fisher_f_distribution(const param_type& par0);
Precondition: 0.0 < m0
&& 0.0 < n0
The first constructor constructs an object whose stored value stored_m
holds the value m0 and whose stored value stored_n
holds the value n0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
fisher_f_distribution::mRealType m() const;
The member function returns the stored value stored_m.
fisher_f_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
fisher_f_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
fisher_f_distribution::nRealType n() const;
The member function returns the stored value stored_n.
fisher_f_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
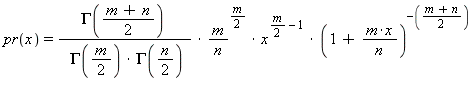
The second member function behaves the same, except that it uses the parameters
stored in par0.
fisher_f_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
fisher_f_distribution::param_typestruct param_type {
typedef fisher_f_distribution<RealType> distribution_type;
param_type(RealType m0 = 1, RealType n0 = 1);
RealType m() const;
RealType n() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
fisher_f_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
fisher_f_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
gamma_distributiontemplate<class RealType = double>
class gamma_distribution {
public:
typedef T1 input_type; [removed with C++11]
typedef RealType result_type;
struct param_type; [added with C++11]
explicit gamma_distribution(result_type alpha0 = result_type(1.0),
result_type beta0 = result_type(1.0)); [beta added with C++11]
explicit gamma_distribution(const param_type& par0); [added with C++11]
result_type alpha() const;
result_type beta() const; [added with C++11]
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const; [added with C++11]
result_type max() const; [added with C++11]
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
result_type stored_alpha; // exposition only
result_type stored_beta; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type with a gamma distribution.
gamma_distribution::alpharesult_type alpha() const;
The member function returns the stored value stored_alpha.
gamma_distribution::betaresult_type beta() const; [added with C++11]
The member function returns the stored value stored_beta.
gamma_distribution::gamma_distributiongamma_distribution(result_type alpha0 = result_type(1.0));
result_type beta0 = result_type(1.0)); [beta added with C++11]
explicit gamma_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 < alpha0
&&0.0 < beta0
The first constructor constructs an object whose stored value stored_alpha
holds the value alpha0 and whose stored value stored_beta
holds the value beta0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
gamma_distribution::input_typetypedef T1 input_type; [removed with C++11]
The type is a synonym for the implementation-defined type T1.
gamma_distribution::maxresult_type max() const; [added with C++11]
The member function returns the largest value returnable by
operator().
gamma_distribution::minresult_type min() const; [added with C++11]
The member function returns the smallest value returnable by
operator().
gamma_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member operator uses the engine eng
as a source of uniformly distributed random values and returns
floating-point values with each value x occurring with probability:
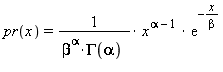
The second member function behaves the same, except that it uses the parameters
stored in par0.
gamma_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
gamma_distribution::param_typestruct param_type { [added with C++11]
typedef gamma_distribution<RealType> distribution_type;
param_type(result_type alpha0 = result_type(1.0),
RealType beta0 result_type(1.0));
RealType alpha() const;
RealType beta() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
gamma_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
gamma_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
generate_canonicaltemplate<class RealType,
size_t bits,
class Engine>
RealType generate_canonical(Engine& gen); [added with C++11]
The template function calls gen() repeatedly and packs the returned
values into a floating-point value x of type RealType until it has
gathered the specified number of mantissa bits in x.
The specified number is the smaller of bits (which must be nonzero)
and the full number of mantissa bits in RealType. The first
call supplies the lowest-order bits. The function returns x.
geometric_distributiontemplate<class IntType = int,
class RealType = double> [always double with C++11]
class geometric_distribution {
public:
typedef T1 input_type; [removed with C++11]
typedef IntType result_type;
struct param_type; [added with C++11]
explicit geometric_distribution(RealType p0 = RealType(0.5));
explicit geometric_distribution(const param_type& par0); [added with C++11]
RealType p() const;
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
RealType stored_p; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type with a geometric distribution.
geometric_distribution::geometric_distributiongeometric_distribution(RealType p0 = RealType(0.5)); explicit geometric_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 < p0 && p0 < 1.0
The first constructor constructs an object whose stored value stored_p holds
the value p0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
geometric_distribution::input_typetypedef T1 input_type; [removed with C++11]
The type is a synonym for the implementation-defined type T1.
geometric_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
geometric_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
geometric_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member function uses the engine eng
as a source of uniformly distributed integral values and returns integral values with
each value i occurring with probability:
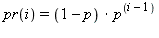
The second member function behaves the same, except that it uses the parameters
stored in par0.
geometric_distribution::pRealType p() const;
The member function returns the stored value stored_p.
geometric_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
geometric_distribution::param_typestruct param_type { [added with C++11]
typedef binomial_distribution<IntType, RealType> distribution_type;
param_type(RealType p0 = RealType(0.5));
RealType p() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
geometric_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
geometric_distribution::result_typetypedef IntType result_type;
The type is a synonym for IntType.
independent_bits_enginetemplate<class Engine,
size_t W, class UIntType>
class independent_bits_engine { [added with C++11]
public:
typedef Engine base_type;
typedef typename base_type::result_type result_type;
independent_bits_engine();
explicit independent_bits_engine(const base_type& eng);
explicit independent_bits_engine(base_type&& eng);
explicit independent_bits_engine(result_type x0);
template<class Seed_seq>
explicit independent_bits_engine(Seed_seq& seq);
void seed();
void seed(result_type x0);
template<class Seed_seq>
void seed(Seed_seq& seq);
const base_type& base() const noexcept;
static constexpr result_type min();
static constexpr result_type max();
result_type operator()();
void discard(unsigned long long count);
private:
Engine stored_eng; // exposition only
int count; // exposition only
};
The template class describes a compound engine
that produces values by repacking bits as needed from the values
returned by its base engine. Each resulting W-bit value
consists of N fields combined as follows:
N0 fields consist of the low-order
W0 bits of values returned by the base engine that are
less than Y0, packed in descending order of significance.
Values that are too large are discarded.N - N0 fields consist of the low-order
W0 + 1 bits of values returned by the base engine that are
less than Y1, packed in descending order of significance.
Values that are too large are discarded.The parameters above (other than W) are determined
as follows:
R is the full range of values returned by the
base engine (stored_eng.max() - stored_eng.min() + 1,
assuming no wraparound occurs.)M is floor(log2(R)).N is initially W / M + (W % M != 0).W0 is W / N.N0 is N - W % N.Y0 is (R >> W0) << W0.Y1 is (R >> W0 + 1) << W0 + 1.Y0 / N < R - Y0 then N is incremented
and the previous four parameters are redetermined.The engine's state is
the state of stored_eng.
The value of the template argument W must be greater than zero
and not greater than the number of bits representable in result_type.
independent_bits_engine::baseconst base_type& base() const noexcept;
The member function returns a reference to the underlying engine object.
independent_bits_engine::base_typetypedef Engine base_type;
The type is a synonym for the type of the underlying engine object.
independent_bits_engine::discardvoid discard(unsigned long long count);
The member function effectively calls (*this)() count times.
independent_bits_engine::independent_bits_engineindependent_bits_engine();
explicit independent_bits_engine(const base_type& eng);
explicit independent_bits_engine(base_type&& eng);
explicit independent_bits_engine(result_type x0);
template<class Seed_seq>
explicit independent_bits_engine(Seed_seq& seq);
The first constructor constructs a independent_bits_engine object with a default-initialized
engine. The second contructor constructs a independent_bits_engine object with a copy of an
engine object. The third contructor constructs a independent_bits_engine object by moving an
engine object. The fourth constructor constructs a independent_bits_engine object with its engine
initialized by stored_engine(x0).
The fifth constructor constructs a
independent_bits_engine object with its engine initialized by
stored_engine(seq).
Unless Seed_seq is not convertible to result_type,
the fifth constructor does not participate in overload resolution.
independent_bits_engine::maxstatic constexpr result_type max();
The static member function returns Engine::max().
independent_bits_engine::minstatic constexpr result_type min();
The static member function returns Engine::min().
independent_bits_engine::operator()result_type operator()();
The member function returns the next value in the sequence.
independent_bits_engine::result_typetypedef typename base_type::result_type result_type;
The type is a synonym for base_type::result_type.
independent_bits_engine::seedvoid seed();
void seed(result_type x0);
template<class Seed_seq>
void seed(Seed_seq& seq);
The first seed function
calls stored_eng.seed().
The second seed function calls stored_eng.seed(x0).
The second seed function calls stored_eng.seed(seq).
Unless Seed_seq is not convertible to result_type,
the third function does not participate in overload resolution.
knuth_btypedef shuffle_order_engine<minstd_rand0, 256>
knuth_b; [added with C++11]
The type is a synonym for a specialization of the template shuffle_order_engine
with a specialization of the template linear_congruential.
linear_congruentialtemplate<class UIntType,
UIntType A, UIntType C, UIntType M>
class linear_congruential {
public:
typedef UIntType result_type;
static constexpr UIntType multiplier = A;
static constexpr UIntType increment = C;
static constexpr UIntType modulus = M;
linear_congruential();
explicit linear_congruential(unsigned long x0);
template<class Gen>
linear_congruential(Gen& gen);
void seed(unsigned long x0 = 1);
template<class Gen>
void seed(Gen& gen);
result_type min() const;
result_type max() const;
result_type operator()();
private:
result_type stored_value; // exposition only
};
The template class describes a simple engine
that produces values of a user-specified unsigned integral type using the
recurrence relation
x(i) = (A * x(i-1) + C) mod M. The engine's
state is the last value returned, or the seed
value if no call has been made to operator().
The template argument UIntType must be
large enough to hold values up to M - 1. The values of the template arguments
A and C must be less than M.
linear_congruential::incrementstatic constexpr UIntType increment = C;
The static const variable holds the value of the template argument C.
linear_congruential::linear_congruentiallinear_congruential();
explicit linear_congruential(unsigned long x0);
template<class Gen>
linear_congruential(Gen& gen);
The first constructor constructs an object and initializes it by calling seed().
The second constructor constructs an object and initializes it by calling seed(x0).
The third constructor constructs an object and initializes it by
calling seed(gen).
linear_congruential::maxresult_type max() const;
The member function returns M - 1.
linear_congruential::minresult_type min() const;
The member function returns C == 0 ? 1 : 0.
linear_congruential::modulusstatic constexpr UIntType modulus = M;
The static const variable holds the value of the template argument M.
linear_congruential::multiplierstatic constexpr UIntType multiplier = A;
The static const variable holds the value of template argument A.
linear_congruential::operator()result_type operator()();
The member function generates a new stored_value by applying
the recurrence relation to the old value of
stored_value.
linear_congruential::result_typetypedef UIntType result_type;
The type is a synonym for UIntType.
linear_congruential::seedvoid seed(unsigned long x0 = 1);
template<class Gen>
void seed(Gen& gen);
The first seed function sets the stored value
stored_value to 1 if C mod M == 0 and
x0 mod M == 0, otherwise it sets the stored value to x0 mod M.
The second seed function calls seed(gen()).
linear_congruential_enginetemplate<class UIntType,
UIntType A, UIntType C, UIntType M>
class linear_congruential_engine { [added with C++11]
public:
typedef UIntType result_type;
static constexpr UIntType multiplier = A;
static constexpr UIntType increment = C;
static constexpr UIntType modulus = M;
static constexpr UIntType default_seed = 1U;
explicit linear_congruential_engine(result_type x0 = default_seed);
template<class Seed_seq>
explicit linear_congruential_engine(Seed_seq& seq);
void seed(result_type x0 = default_seed);
template<class Seed_seq>
void seed(Seed_seq& seq);
static constexpr result_type min();
static constexpr result_type max();
result_type operator()();
void discard(unsigned long long count)();
private:
result_type stored_value; // exposition only
};
The template class describes a simple engine
that produces values of a user-specified unsigned integral type using the
recurrence relation
x(i) = (A * x(i-1) + C) mod M. The engine's
state is the last value returned, or the seed
value if no call has been made to operator().
The template argument UIntType must be
large enough to hold values up to M - 1. The values of the template arguments
A and C must be less than M.
linear_congruential_engine::default_seedstatic constexpr UIntType default_seed = 1U;
The static const variable holds the default seed value 1U.
linear_congruential_engine::discardvoid discard(unsigned long long count);
The member function effectively calls (*this)() count times.
linear_congruential_engine::incrementstatic constexpr UIntType increment = C;
The static const variable holds the value of the template argument C.
linear_congruential_engine::linear_congruential_engineexplicit linear_congruential_engine(result_type x0 = default_seed);
template<class Seed_seq>
explicit linear_congruential_engine(Seed_seq& seq);
The first constructor constructs an object and initializes it by calling seed(x0).
The second constructor constructs an object and initializes it by calling seed(seq).
Unless Seed_seq is not convertible to result_type,
the second constructor does not participate in overload resolution.
linear_congruential_engine::maxstatic constexpr result_type max();
The static member function returns M - 1.
linear_congruential_engine::minstatic constexpr result_type min() const;
The static member function returns C == 0 ? 1 : 0.
linear_congruential_engine::modulusstatic constexpr UIntType modulus = M;
The static const variable holds the value of the template argument M.
linear_congruential_engine::multiplierstatic constexpr UIntType multiplier = A;
The static const variable holds the value of template argument A.
linear_congruential_engine::operator()result_type operator()();
The member function generates a new stored_value by applying
the recurrence relation to the old value of
stored_value.
linear_congruential_engine::result_typetypedef UIntType result_type;
The type is a synonym for UIntType.
linear_congruential_engine::seedvoid seed(result_type x0 = default_seed);
template<class Seed_seq>
void seed(Seed_seq& seq);
The first seed function sets the stored value
stored_value to 1 if C mod M == 0 and
x0 mod M == 0, otherwise it sets the stored value to x0 mod M.
The second seed function calls seed(x),
where x is determined as follows:
k is the number of unsigned long integers needed to supply
all the bits in a UIntType integer (at least 1).a is an array of 3 + k elements of type UIntType.a is initialized by calling
seq.generate(&a[0], &a[3 + k]).x is composed by packing the k
elements beginning at a[3], which supplies the lowest-order bits.Unless Seed_seq is not convertible to result_type,
the second function does not participate in overload resolution.
lognormal_distributiontemplate<class RealType = double>
class lognormal_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit lognormal_distribution(result_type m0 = result_type(0.0),
result_type s0 = result_type(1.0));
explicit lognormal_distribution(const param_type& par0);
result_type m() const;
result_type s() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_a; // exposition only
result_type stored_b; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with a log normal distribution.
lognormal_distribution::lognormal_distributionlognormal_distribution(result_type m0 = result_type(0.0),
result_type s0 = result_type(1.0));
explicit lognormal_distribution(const param_type& par0);
Precondition: 0.0 < s0
The first constructor constructs an object whose stored value stored_m
holds the value m0 and whose stored value stored_s holds
the value s0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
lognormal_distribution::mresult_type m() const;
The member function returns the stored value stored_m.
lognormal_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
lognormal_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
lognormal_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
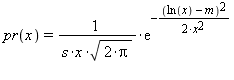
The second member function behaves the same, except that it uses the parameters
stored in par0.
lognormal_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
lognormal_distribution::param_typestruct param_type {
typedef lognormal_distribution<RealType> distribution_type;
param_type(result_type m0 = result_type(0.0),
result_type s0 = result_type(1.0));
result_type m() const;
result_type s() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
lognormal_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
lognormal_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
lognormal_distribution::sresult_type s() const;
The member function returns the stored value stored_s.
mersenne_twistertemplate<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
class mersenne_twister {
public:
typedef UIntType result_type;
static constexpr int word_size = W;
static constexpr int state_size = N;
static constexpr int shift_size = M;
static constexpr int mask_bits = R;
static constexpr UIntType parameter_a = A;
static constexpr int output_u = U;
static constexpr int output_s = S;
static constexpr UIntType output_b = B;
static constexpr int output_t = T;
static constexpr UIntType output_c = C;
static constexpr int output_l = L;
mersenne_twister();
explicit mersenne_twister(unsigned long x0);
template<class Gen>
mersenne_twister(Gen& gen);
void seed();
void seed(unsigned long x0);
template<class Gen>
void seed(Gen& gen);
result_type min() const;
result_type max() const;
result_type operator()();
};
The template class describes a simple engine.
It holds a large integral value with W * (N - 1) + R bits.
It extracts W bits at a time from this large value, and when it
has used all the bits it twists the large value by shifting and mixing the bits so that it has
a new set of bits to extract from. The engine's state is the
last N W-bit values used if operator()
has been called at least N times, otherwise the M
W-bit values that have been used and
the last N - M values of the
seed.
The template argument UIntType must be
large enough to hold values up to 2W - 1. The values of the
other template arguments must satisfy the following requirements:
1 < M <= N0 <= R, U, S, T, L <= W0 <= A, B, C <= 2W - 1W * (N - 1) + R must be a Mersenne primeThe generator twists the large value that it holds by executing the following code:
for (int i = 0; i < N; ++i)
{ // twist
temp = (x[i] & LMASK) << (W - 1) | (x[i + 1] & HMASK) >> 1;
if (temp & 1)
y[i] = (temp >> 1) ^ A ^ x[(i + R) % N];
else
y[i] = (temp >> 1) ^ x[(i + R) % N];
}
for (int i = 0; i < N; ++i)
x[i] = y[i];
where LMASK is an unsigned W-bit value with its
low R bits set to 1 and the rest of its bits set to 0,
and HMASK is the complement of LMASK.
The generator holds a current index idx initialized to 0.
It extracts bits
by executing the following code:
temp = x[idx++];
temp = temp ^ (temp >> U);
temp = temp ^ ((temp << S) & B);
temp = temp ^ ((temp << T) & C);
temp = temp ^ (temp >> L);
When idx reaches N the generator
twists the stored value
and sets idx back to 0.
mersenne_twister::mask_bitsstatic constexpr int mask_bits = R;
The static const variable holds the value of the template argument R.
mersenne_twister::maxresult_type max() const;
The member function returns the largest value in the generated sequence.
mersenne_twister::mersenne_twistermersenne_twister();
explicit mersenne_twister(unsigned long x0);
template<class Gen>
mersenne_twister(Gen& gen);
The first constructor constructs an object and initializes it by calling seed().
The second constructor constructs an object and initializes it by calling seed(x0).
The third constructor constructs an object and initializes it by
calling seed(gen).
mersenne_twister::minresult_type min() const;
The member function returns zero.
mersenne_twister::operator()result_type operator()();
The member function extracts the next value in the sequence and returns it.
mersenne_twister::output_bstatic constexpr UIntType output_b = B;
The static const variable holds the value of the template argument B.
mersenne_twister::output_cstatic constexpr UIntType output_c = C;
The static const variable holds the value of the template argument C.
mersenne_twister::output_lstatic constexpr int output_l = L;
The static const variable holds the value of the template argument L.
mersenne_twister::output_sstatic constexpr int output_s = S;
The static const variable holds the value of the template argument S.
mersenne_twister::output_tstatic constexpr int output_t = T;
The static const variable holds the value of the template argument T.
mersenne_twister::output_ustatic constexpr int output_u = U;
The static const variable holds the value of the template argument U.
mersenne_twister::parameter_astatic constexpr UIntType parameter_a = A;
The static const variable holds the value of the template argument A.
mersenne_twister::result_typetypedef UIntType result_type;
The type is a synonym for UIntType.
mersenne_twister::seedtemplate<class Gen>
void seed(Gen& gen);
void seed();
void seed(unsigned long x0);
Precondition: 0 < x0
The first seed function
generates N values
from the values of type unsigned long returned by successive invocations of
gen and then twists
the resulting large integer value. Each value is gen() % 2W.
The second seed function calls seed(4357).
The third seed function sets the oldest historical value h[0] to
x0 mod 2W, then iteratively sets each successive historical value
h[i] to (i + 1812433253 * (h[i - 1] >> (W - 2))) mod 2W,
for i ranging from 1 to N - 1.
mersenne_twister::shift_sizestatic constexpr int shift_size = M;
The static const variable holds the value of the template argument M.
mersenne_twister::state_sizestatic constexpr int state_size = N;
The static const variable holds the value of the template argument N.
mersenne_twister::word_sizestatic constexpr int word_size = W;
The static const variable holds the value of the template argument W.
mersenne_twister_enginetemplate<class UIntType,
size_t W, size_t N, size_t M, size_t R,
UIntType A, size_t U,
UIntType D, size_t S,
UIntType B, size_t T,
UIntType C, size_t L
UIntType F>
class mersenne_twister_engine { [added with C++11]
public:
typedef UIntType result_type;
static constexpr size_t word_size = W;
static constexpr size_t state_size = N;
static constexpr size_t shift_size = M;
static constexpr size_t mask_bits = R;
static constexpr UIntType xor_mask = A;
static constexpr size_t tempering_u = U;
static constexpr size_t tempering_d = D;
static constexpr size_t tempering_s = S;
static constexpr UIntType tempering_b = B;
static constexpr size_t tempering_t = T;
static constexpr UIntType tempering_c = C;
static constexpr size_t tempering_l = L;
static constexpr UIntType initialization_multiplier = C;
static constexpr result_type default_seed = 5489U;
explicit mersenne_twister_engine(unsigned long x0 = default_seed);
template<class Seed_seq>
explicit mersenne_twister_engine(Seed_seq& seq);
void seed(unsigned long x0 = default_seed);
template<class Seed_seq>
void seed(Seed_seq& seq);
result_type min() const;
result_type max() const;
result_type operator()();
void discard(unsigned long long count)();
};
The template class describes a simple engine.
It holds a large integral value with W * (N - 1) + R bits.
It extracts W bits at a time from this large value, and when it
has used all the bits it twists the large value by shifting and mixing the bits so that it has
a new set of bits to extract from. The engine's state is the
last N W-bit values used if operator()
has been called at least N times, otherwise the M
W-bit values that have been used and
the last N - M values of the
seed.
The template argument UIntType must be
large enough to hold values up to 2W - 1. The values of the
other template arguments must satisfy the following requirements:
0 < M <= N0 <= {R, 2 * U, S, T, L} <= W0 <= {A, B, C, D, F} <= 2W - 1W * (N - 1) + R must be a Mersenne primeThe generator twists the large value that it holds by executing the following code:
for (size_t i = 0; i < N; ++i)
{ // twist
temp = (x[i] & LMASK) << (W - 1) | (x[i + 1] & HMASK) >> 1;
if (temp & 1)
y[i] = (temp >> 1) ^ A ^ x[(i + R) % N];
else
y[i] = (temp >> 1) ^ x[(i + R) % N];
}
for (size_t i = 0; i < N; ++i)
x[i] = y[i];
where LMASK is an unsigned W-bit value with its
low R bits set to 1 and the rest of its bits set to 0,
and HMASK is the complement of LMASK.
The generator holds a current index idx initialized to 0.
It extracts bits
by executing the following code:
temp = x[idx++];
temp = temp ^ ((temp >> U) & D);
temp = temp ^ ((temp << S) & B);
temp = temp ^ ((temp << T) & C);
temp = temp ^ (temp >> L);
When idx reaches N the generator
twists the stored value
and sets idx back to 0.
mersenne_twister_engine::default_seedstatic constexpr result_type default_seed = 5489U;
The static const variable holds the default seed value 5489U.
mersenne_twister_engine::discardvoid discard(unsigned long long count);
The member function effectively calls (*this)() count times.
mersenne_twister_engine::initialization_multiplierstatic constexpr UIntType initialization_multiplier = F;
The static const variable holds the value of the template argument F.
mersenne_twister_engine::mask_bitsstatic constexpr size_t mask_bits = R;
The static const variable holds the value of the template argument R.
mersenne_twister_engine::maxresult_type max() const;
The member function returns the largest value in the generated sequence.
mersenne_twister_engine::mersenne_twister_engineexplicit mersenne_twister_engine(unsigned long x0 = default_seed);
template<class Seed_seq>
explicit mersenne_twister_engine(Seed_seq& seq);
The first constructor constructs an object and initializes it by calling seed(x0).
The second constructor constructs an object and initializes it by calling seed(seq).
Unless Seed_seq is not convertible to result_type,
the second constructor does not participate in overload resolution.
mersenne_twister_engine::minresult_type min() const;
The member function returns zero.
mersenne_twister_engine::operator()result_type operator()();
The member function extracts the next value in the sequence and returns it.
mersenne_twister_engine::tempering_bstatic constexpr UIntType tempering_b = B;
The static const variable holds the value of the template argument B.
mersenne_twister_engine::tempering_cstatic constexpr UIntType tempering_c = C;
The static const variable holds the value of the template argument C.
mersenne_twister_engine::tempering_dstatic constexpr UIntType tempering_d = D;
The static const variable holds the value of the template argument D.
mersenne_twister_engine::tempering_lstatic constexpr size_t tempering_l = L;
The static const variable holds the value of the template argument L.
mersenne_twister_engine::tempering_sstatic constexpr size_t tempering_s = S;
The static const variable holds the value of the template argument S.
mersenne_twister_engine::tempering_tstatic constexpr size_t tempering_t = T;
The static const variable holds the value of the template argument T.
mersenne_twister_engine::tempering_ustatic constexpr size_t tempering_u = U;
The static const variable holds the value of the template argument U.
mersenne_twister_engine::result_typetypedef UIntType result_type;
The type is a synonym for UIntType.
mersenne_twister_engine::seedvoid seed(result_type x0 = default_seed);
template<class Seed_seq>
void seed(Seed_seq& seq);
Precondition: 0 < x0
The first seed function sets the oldest historical value h[0] to
x0 mod 2W, then iteratively sets each successive historical value
h[i] to (i + F * (h[i - 1] >> (W - 2))) mod 2W,
for i ranging from 1 to N - 1.
The second seed function sets the N historical values beginning with
h[0] as follows:
k is the number of unsigned long integers needed to supply
all the bits in a UIntType integer (at least 1).a is an array of N * k elements of type UIntType.a is initialized by calling
seq.generate(&a[0], &a[N * k]).h[i] is composed by packing the k
elements beginning at a[i * k], which supplies the lowest-order bits.Unless Seed_seq is not convertible to result_type,
the second function does not participate in overload resolution.
mersenne_twister_engine::shift_sizestatic constexpr size_t shift_size = M;
The static const variable holds the value of the template argument M.
mersenne_twister_engine::state_sizestatic constexpr size_t state_size = N;
The static const variable holds the value of the template argument N.
mersenne_twister_engine::word_sizestatic constexpr size_t word_size = W;
The static const variable holds the value of the template argument W.
mersenne_twister_engine::xor_maskstatic constexpr UIntType xor_mask = A;
The static const variable holds the value of the template argument A.
minstd_randtypedef linear_congruential_engine< ui-type, 48271, 0, 2147483647> minstd_rand;
The type is a synonym for a specialization of the template linear_congruential_engine.
minstd_rand0typedef linear_congruential_engine< ui-type, 16807, 0, 2147483647> minstd_rand0;
The type is a synonym for a specialization of the template linear_congruential_engine.
mt19937typedef mersenne_twister< ui-type, 32, 624, 397, 31,
0x9908b0df, 11, 7, 0x9d2c5680, 15, 0xefc60000, 18> mt19937;
The type is a synonym for a specialization of the template mersenne_twister.
mt19937_64typedef mersenne_twister_engine<ui-type, 64, 312, 156, 31,
0xb5026f5aa96619e9ULL, 29, 0x5555555555555555ULL, 17,
0x71d67fffeda60000ULL, 37, 0xfff7eee000000000ULL, 43,
6364136223846793005ULL> mt19937_64 [added with C++11];
The type is a synonym for a specialization of the template mersenne_twister_engine.
negative_binomial_distributiontemplate<class IntType = int>
class negative_binomial_distribution { [added with C++11]
public:
typedef IntType result_type;
struct param_type;
explicit negative_binomial_distribution(result_type k0 = 1,
double p0 = 0.5);
explicit negative_binomial_distribution(const param_type& par0);
result_type k() const;
double p() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_k; // exposition only
double stored_p; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type distributed with a binomial distribution.
negative_binomial_distribution::kresult_type k() const;
The member function returns the stored value stored_k.
negative_binomial_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
negative_binomial_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
negative_binomial_distribution::negative_binomial_distributionnegative_binomial_distribution(result_type k0 = 1,
double p0 = 0.5);
explicit negative_binomial_distribution(const param_type& par0);
Precondition: 0.0 < k0 && 0.0 < p0 && p0 <= 1.0
The first constructor constructs an object whose stored value stored_p
holds the value p0 and whose stored value stored_k holds
the value k0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
negative_binomial_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
integral values with each value i occurring with probability:
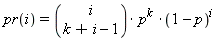
The second member function behaves the same, except that it uses the parameters
stored in par0.
negative_binomial_distribution::pdouble p() const;
The member function returns the stored value stored_p.
negative_binomial_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
negative_binomial_distribution::param_typestruct param_type {
typedef negative_binomial_distribution<IntType> distribution_type;
param_type(result_type t0 = 1, double p0 = 0.5);
result_type k() const;
double p() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
negative_binomial_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
negative_binomial_distribution::result_typetypedef IntType result_type;
The type is a synonym for IntType.
normal_distributiontemplate<class RealType = double>
class normal_distribution {
public:
typedef T1 input_type; [removed with C++11]
typedef RealType result_type;
struct param_type; [added with C++11]
explicit normal_distribution(result_type mean0 = result_type(0.0),
result_type sigma0 = result_type(1.0));
explicit normal_distribution(const param_type& par0); [added with C++11]
result_type mean() const;
result_type sigma() const;
result_type stddev() const; [added with C++11]
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const; [added with C++11]
result_type max() const; [added with C++11]
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
result_type stored_mean; // exposition only
result_type stored_sigma; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type with a normal distribution.
normal_distribution::input_typetypedef T1 input_type; [removed with C++11]
The type is a synonym for the implementation-defined type T1.
normal_distribution::maxresult_type max() const; [added with C++11]
The member function returns the largest value returnable by
operator().
normal_distribution::meanresult_type mean() const;
The member function returns the stored value stored_mean.
normal_distribution::minresult_type min() const; [added with C++11]
The member function returns the smallest value returnable by
operator().
normal_distribution::normal_distributionnormal_distribution(result_type mean0 = result_type(0.0),
result_type sigma0 = result_type(1.0));
explicit normal_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 < sigma0
The first constructor constructs an object whose stored value stored_mean
holds the value mean0 and whose stored value stored_sigma
holds the value sigma0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
normal_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member operator uses the engine eng
as a source of uniformly distributed random values and returns
floating-point values with each value x occurring with probability:
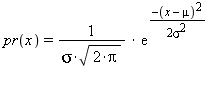
normal_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
normal_distribution::param_typestruct param_type { [added with C++11]
typedef normal_distribution<RealType> distribution_type;
param_type(result_type mean0 = result_type(0.0),
RealType sigma0 = result_type(1.0));
RealType mean() const;
RealType sigma() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
normal_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
normal_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
normal_distribution::sigmaresult_type sigma() const;
The member function returns the stored value stored_sigma.
normal_distribution::stddevresult_type stddev() const; [added with C++11]
The member function returns the stored value stored_sigma.
operator!=template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator!=(
const linear_congruential<UIntType, A, C, M>& left,
const linear_congruential<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator!=(
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& left,
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class IntType,
IntType M, int S, int R>
bool operator!=(
const subtract_with_carry<IntType, M, S, R>& left,
const subtract_with_carry<IntType, M, S, R>& right);
template<class RealType,
int W, int S, int R>
bool operator!=(
const subtract_with_carry_01<RealType, W, S, R>& left,
const subtract_with_carry_01<RealType, W, S, R>& right);
template<class Engine,
int P, int R>
bool operator!=(
const discard_block<Engine, F, R>& left,
const discard_block<Engine, F, R>& right);
template<class Engine1, int S1,
class Engine2, int S2>
bool operator!=(
const xor_combine<Engine1, S1, Engine2, S2>& left,
const xor_combine<Engine1, S1, Engine2, S2>& right);
template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator!=( [added with C++11]
const linear_congruential_engine<UIntType, A, C, M>& left,
const linear_congruential_engine<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator!=( [added with C++11]
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& left,
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class IntType,
IntType M, int S, int R>
bool operator!=( [added with C++11]
const subtract_with_carry_engine<IntType, A, C, M>& left,
const subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Engine,
size_t P, size_t R>
bool operator!=( [added with C++11]
const discard_block_engine<Engine, F, R>& left,
const discard_block_engine<Engine, F, R>& right);
template<class Engine,
size_t W, class UIntType>
bool operator!=( [added with C++11]
const independent_bits_engine<Engine, W, U>& left,
const independent_bits_engine<Engine, W, U>& right);
template<class Engine,
size_t K>
bool operator!=( [added with C++11]
const ahuffle_order_engine<Engine, K>& left,
const shuffle_order_engine<Engine, K>& right);
The template operators return !(left == right).
operator==template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator==(
const linear_congruential<UIntType, A, C, M>& left,
const linear_congruential<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator==(
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& left,
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class IntType,
IntType M, int S, int R>
bool operator==(
const subtract_with_carry<IntType, M, S, R>& left,
const subtract_with_carry<IntType, M, S, R>& right);
template<class RealType,
int W, int S, int R>
bool operator==(
const subtract_with_carry_01<RealType, W, S, R>& left,
const subtract_with_carry_01<RealType, W, S, R>& right);
template<class Engine,
int P, int R>
bool operator==(
const discard_block<Engine, F, R>& left,
const discard_block<Engine, F, R>& right);
template<class Engine1, int S1,
class Engine2, int S2>
bool operator==(
const xor_combine<Engine1, S1, Engine2, S2>& left,
const xor_combine<Engine1, S1, Engine2, S2>& right);
template<class UIntType,
UIntType A, UIntType C, UIntType M>
bool operator==( [added with C++11]
const linear_congruential_engine<UIntType, A, C, M>& left,
const linear_congruential_engine<UIntType, A, C, M>& right);
template<class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
bool operator==( [added with C++11]
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& left,
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class IntType,
IntType M, int S, int R>
bool operator==( [added with C++11]
const subtract_with_carry_engine<IntType, A, C, M>& left,
const subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Engine,
size_t P, size_t R>
bool operator==( [added with C++11]
const discard_block_engine<Engine, F, R>& left,
const discard_block_engine<Engine, F, R>& right);
template<class Engine,
size_t W, class UIntType>
bool operator==( [added with C++11]
const independent_bits_engine<Engine, W, U>& left,
const independent_bits_engine<Engine, W, U>& right);
template<class Engine,
size_t K>
bool operator==( [added with C++11]
const ahuffle_order_engine<Engine, K>& left,
const shuffle_order_engine<Engine, K>& right);
The template operators return true if their engine operands have the same stored parameters and state. (They generate the same sequence.)
operator<<template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const linear_congruential<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const subtract_with_carry<IntType, M, S, R>& right);
template<class Elem, class Traits, class RealType,
int W, int S, int R>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const subtract_with_carry_01<RealType, W, S, R>& right);
template<class Elem, class Traits, class Engine,
int P, int R>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const discard_block<Engine, F, R>& right);
template<class Elem, class Traits, class Engine1, int S1,
class Engine2, int S2>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const xor_combine<Engine1, S1, Engine2, S2>& right);
template<class Elem, class Traits>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const bernoulli_distribution& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const binomial_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const exponential_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const gamma_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const geometric_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const normal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const poisson_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const uniform_int<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<(
basic_ostream<Elem, Traits>& ostr,
const uniform_real<RealType>& right);
template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const linear_congruential_engine<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Elem, class Traits, class Engine,
size_t P, size_t R>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const discard_block_engine<Engine, F, R>& right);
template<class Elem, class Traits, class Engine,
size_t W, class UIntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const independent_bits_engine<Engine, W, U>& right);
template<class Elem, class Traits, class Engine,
size_t K>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const shuffle_order_engine<Engine, K>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const cauchy_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const chi_squared_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const discrete_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const extreme_value_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const fisher_f_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const lognormal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const negative_binomial_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const piecewise_constant_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const student_t_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const uniform_int_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const uniform_real_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_ostream<Elem, Traits>& operator<<( [added with C++11]
basic_ostream<Elem, Traits>& ostr,
const weibull_distribution<RealType>& right);
The template function inserts into the stream ostr
sufficient information about right to restore its stored
parameters with a subsequent extract. The stream must insert integer
values as decimals.
operator>>template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
linear_congruential<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
mersenne_twister<UIntType, W, N, M, R,
A, U, S, B, T, C, L>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
subtract_with_carry<IntType, M, S, R>& right);
template<class Elem, class Traits, class RealType,
int W, int S, int R>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
subtract_with_carry_01<RealType, W, S, R>& right);
template<class Elem, class Traits, class Engine,
int P, int R>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
discard_block<Engine, F, R>& right);
template<class Elem, class Traits, class Engine1, int S1,
class Engine2, int S2>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
xor_combine<Engine1, S1, Engine2, S2>& right);
template<class Elem, class Traits>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
bernoulli_distribution& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
binomial_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
exponential_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
gamma_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
geometric_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
normal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType
class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
poisson_distribution<IntType, RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
uniform_int<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>(
basic_istream<Elem, Traits>& ostr,
uniform_real<RealType>& right);
template<class Elem, class Traits, class UIntType,
UIntType A, UIntType C, UIntType M>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
linear_congruential_engine<UIntType, A, C, M>& right);
template<class Elem, class Traits, class UIntType,
int W, int N, int M, int R,
UIntType A, int U, int S,
UIntType B, int T, UIntType C, int L>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
mersenne_twister_engine<UIntType, W, N, M, R,
A, U, D, S, B, T, C, L, F>& right);
template<class Elem, class Traits, class IntType,
IntType M, int S, int R>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
subtract_with_carry_engine<IntType, A, C, M>& right);
template<class Elem, class Traits, class Engine,
size_t P, size_t R>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
discard_block_engine<Engine, F, R>& right);
template<class Elem, class Traits, class Engine,
size_t W, class UIntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
independent_bits_engine<Engine, W, U>& right);
template<class Elem, class Traits, class Engine,
size_t K>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
shuffle_order_engine<Engine, K>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
cauchy_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
chi_squared_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
discrete_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
extreme_value_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
fisher_f_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
lognormal_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
negative_binomial_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
piecewise_constant_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
student_t_distribution<RealType>& right);
template<class Elem, class Traits, class IntType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
uniform_int_distribution<IntType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
uniform_real_distribution<RealType>& right);
template<class Elem, class Traits, class RealType>
basic_istream<Elem, Traits>& operator>>( [added with C++11]
basic_istream<Elem, Traits>& ostr,
weibull_distribution<RealType>& right);
The template function extracts from the stream istr
sufficient information into right to restore its stored
parameters from a previous insert. The stream must extract integer
values as decimals.
piecewise_constant_distributiontemplate<class RealType = double>
class piecewise_constant_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
piecewise_constant_distribution();
template<class InIt1, class InIt2>
piecewise_constant_distribution(InIt1 first1, InIt1 last1,
InIt2 first2);
template<class Fn>
piecewise_constant_distribution(initializer_list<RealType> init, Fn func);
template<class Fn>
piecewise_constant_distribution(size_t count,
double low, double high, Fn func);
explicit piecewise_constant_distribution(const param_type& par0);
vector<result_type> densities() const;
vector<RealType> intervals() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
vector<result_type> stored_p; // exposition only
vector<RealType> stored_x; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed according to a varying-width histogram of probabilities.
Three distributions are very similar:
discrete_distribution
has uniform-width intervals with uniform probability in each interval.piecewise_constant_distribution
has varying-width intervals with uniform probability in each interval.piecewise_linear_distribution
has varying-width intervals with linearly varying probability over each interval.piecewise_constant_distribution::densitiesvector<result_type> densities() const;
The member function returns the stored value stored_p,
with each element stored_p[I] divided by stored_x[I + 1]
- stored_x[I].
piecewise_constant_distribution::intervalsvector<RealType> intervals() const;
The member function returns the stored value stored_x.
piecewise_constant_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
piecewise_constant_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
piecewise_constant_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x in the range [stored_x.front(),
stored_x.back()) occurring with probability determined by the smallest element
I for which x < stored_x[I + 1}, and other values of x
occurring with probability zero. Values x are uniformly distributed over the
range [stored_x[I], stored_x[I + 1]) with total probability stored_p[I].
The second member function behaves the same, except that it uses the parameters
stored in par0.
piecewise_constant_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
piecewise_constant_distribution::param_typestruct param_type {
typedef piecewise_constant_distribution<RealType> distribution_type;
param_type();
template<class InIt1, class InIt2>
param_type(InIt1 first1, InIt1 last1,
InIt2 first2);
template<class Fn>
param_type(initializer_list<RealType> init, Fn func);
template<class Fn>
param_type(size_t count,
double low, double high, Fn func);
vector<result_type> densities() const;
vector<RealType> intervals() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
piecewise_constant_distribution::piecewise_constant_distributionpiecewise_constant_distribution();
template<class InIt1, class InIt2>
piecewise_constant_distribution(InIt1 first1, InIt1 last1,
InIt2 first2);
template<class Fn>
piecewise_constant_distribution(initializer_list<RealType> init, Fn func);
template<class Fn>
piecewise_constant_distribution(size_t count,
double low, double high, Fn func);
explicit piecewise_constant_distribution(const param_type& par0);
Precondition: All elements to be stored in
stored_p are nonnegative and at least one is nonzero.
The first constructor constructs an object whose stored value stored_x
holds the values RealType(0.0) and RealType(1.0),
and whose stored value stored_p holds the value 1.0.
The second constructor constructs an object whose stored value stored_x
is initialized with the sequence [first1, last1).
If the sequence has fewer than two elements, stored_x has two
elements RealType(0.0) and RealType(1.0), and
stored_p has one element with value 1.
Otherwise, stored_p is initialized with stored_x.size() - 1
elements beginning at first2, then normalized so that the sum of
all elements is 1.
The third constructor constructs an object whose stored value stored_x
is initialized with the sequence [init.begin(), init.end()).
Its stored value stored_p is initialized with init.size() - 1 elements,
where element I stores the value func(x) for x
in the middle of subrange [stored_x[I], stored_x[I + 1]].
If count < 1, stored_p has one element with
value 1.
The fourth constructor constructs an object whose stored value stored_p
is initialized with count elements. It divides the range high - low
into count subranges, then stores in element I
the value func(x) for x in the middle of subrange I.
It stores in stored_x the count + 1 endpoints of these
subranges.
If count < 1, stored_p has one element with
value 1.
The fifth constructor constructs an object whose stored parameters
are initialized from par0.
piecewise_constant_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
piecewise_constant_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
piecewise_linear_distributiontemplate<class RealType = double>
class piecewise_linear_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
piecewise_linear_distribution();
template<class InIt1, class InIt2>
piecewise_linear_distribution(InIt1 first1, InIt1 last1,
InIt2 first2);
template<class Fn>
piecewise_linear_distribution(initializer_list<RealType> init, Fn func);
template<class Fn>
piecewise_linear_distribution(size_t count,
double low, double high, Fn func);
explicit piecewise_linear_distribution(const param_type& par0);
vector<result_type> densities() const;
vector<RealType> intervals() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
vector<result_type> stored_p; // exposition only
vector<RealType> stored_x; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed according to a varying-width histogram of probabilities, with probability varying linearly over each interval.
Three distributions are very similar:
discrete_distribution
has uniform-width intervals with uniform probability in each interval.piecewise_constant_distribution
has varying-width intervals with uniform probability in each interval.piecewise_linear_distribution
has varying-width intervals with linearly varying probability over each interval.piecewise_linear_distribution::densitiesvector<result_type> densities() const;
The member function returns the stored value stored_p.
piecewise_linear_distribution::intervalsvector<RealType> intervals() const;
The member function returns the stored value stored_x.
piecewise_linear_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
piecewise_linear_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
piecewise_linear_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x in the range [stored_x.front(),
stored_x.back()) occurring with probability determined by the smallest element
I for which x < stored_x[I + 1}, and other values of x
occurring with probability zero. Values x are uniformly distributed over the
range [stored_x[I], stored_x[I + 1]) with probability varying from
stored_p[I] to stored_p[I + 1].
The second member function behaves the same, except that it uses the parameters
stored in par0.
piecewise_linear_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
piecewise_linear_distribution::param_typestruct param_type {
typedef piecewise_linear_distribution<RealType> distribution_type;
param_type();
template<class InIt1, class InIt2>
param_type(InIt1 first1, InIt1 last1,
InIt2 first2);
template<class Fn>
param_type(initializer_list<RealType> init, Fn func);
template<class Fn>
param_type(size_t count,
double low, double high, Fn func);
vector<result_type> densities() const;
vector<RealType> intervals() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
piecewise_linear_distribution::piecewise_linear_distributionpiecewise_linear_distribution();
template<class InIt1, class InIt2>
piecewise_linear_distribution(InIt1 first1, InIt1 last1,
InIt2 first2);
template<class Fn>
piecewise_linear_distribution(initializer_list<RealType> init, Fn func);
template<class Fn>
piecewise_linear_distribution(size_t count,
double low, double high, Fn func);
explicit piecewise_linear_distribution(const param_type& par0);
Precondition: All elements to be stored in
stored_p are nonnegative and at least one is nonzero.
The first constructor constructs an object whose stored value stored_x
holds the values RealType(0.0) and RealType(1.0),
and whose stored value stored_p holds the values 1.0
and 1.0.
The second constructor constructs an object whose stored value stored_x
is initialized with the sequence [first1, last1).
stored_p is initialized with stored_x.size()
elements beginning at first2.
The third constructor constructs an object whose stored value stored_x
is initialized with the sequence [init.begin(), init.end()).
Its stored value stored_p is initialized with init.size() elements,
where element I stores the value func(stored_x[I]).
The fourth constructor constructs an object whose stored value stored_p
is initialized with count elements. It divides the range high - low
into count subranges, then stores in element I
the value func(x) for x in the middle of subrange I.
It stores in stored_x the count + 1 endpoints of these
subranges.
The fifth constructor constructs an object whose stored parameters
are initialized from par0.
In all cases,
if the sequence has fewer than two elements, stored_x has two
elements RealType(0.0) and RealType(1.0), and
stored_p has two elements with value 1.
Also, stored_p is normalized so that the sum of
all probability intervals is 1.
piecewise_linear_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
piecewise_linear_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
poisson_distributiontemplate<class IntType = int,
class RealType = double> [always double with C++11]
class poisson_distribution {
public:
typedef T1 input_type; [removed with C++11]
typedef IntType result_type;
struct param_type; [added with C++11]
explicit poisson_distribution(RealType mean0 = RealType(1.0));
explicit poisson_distribution(const param_type& par0); [added with C++11]
RealType mean() const;
param_type param() const; [added with C++11]
void param(const param_type& par0); [added with C++11]
result_type min() const; [added with C++11]
result_type max() const; [added with C++11]
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
private:
RealType stored_mean; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type with a Poisson distribution.
poisson_distribution::input_typetypedef T1 input_type; [removed with C++11]
The type is a synonym for the implementation-defined type T1.
poisson_distribution::maxresult_type max() const; [added with C++11]
The member function returns the largest value returnable by
operator().
poisson_distribution::meanRealType mean() const;
The member function returns the stored value stored_mean.
poisson_distribution::minresult_type min() const; [added with C++11]
The member function returns the smallest value returnable by
operator().
poisson_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0); [added with C++11]
The first member operator uses the engine eng
as a source of uniformly distributed integral values and returns integral values with
each value i occurring with probability:
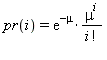
The second member function behaves the same, except that it uses the parameters
stored in par0.
poisson_distribution::paramparam_type param() const; [added with C++11] void param(const param_type& par0); [added with C++11]
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
poisson_distribution::param_typestruct param_type { [added with C++11]
typedef poisson_distribution<IntType, RealType> distribution_type;
param_type(RealType mean = RealType(1.0));
RealType mean() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
poisson_distribution::poisson_distributionpoisson_distribution(RealType mean0 = RealType(1.0)); explicit binomial_distribution(const param_type& par0); [added with C++11]
Precondition: 0.0 < mean0
The first constructor constructs an object whose stored value stored_mean
holds the value mean0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
poisson_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
poisson_distribution::result_typetypedef IntType result_type;
The type is a synonym for IntType.
random_deviceclass random_device {
public:
typedef unsigned int result_type;
explicit random_device(const string& token = /* implementation defined */);
result_type min() const;
result_type max() const;
double entropy() const noexcept;
result_type operator()();
private:
random_device(const random_device&) = delete; [added with C++11]
void operator=(const random_device&) = delete; [added with C++11]
};
The class describes a source of random numbers, preferably from a
non-deterministic external device. In this implementation
the values produced by default are not non-deterministic.
They are uniformly distributed in the closed range [0, 65535].
random_device::entropydouble entropy() const noexcept;
The member function returns an estimate of the randomness of the source, as measured in bits. (In the extreme, a non-random source has an entropy of zero.)
random_device::maxresult_type max() const;
The member function returns the largest value returned by the source.
random_device::minresult_type min() const;
The member function returns the smallest value returned by the source.
random_device::operator()result_type operator()();
The member function returns values uniformly distributed in the closed interval [min(), max()].
random_device::random_devicerandom_device(const string& str = /* implementation defined */);
The constructor initializes the device (as needed) with str.
random_device::result_typetypedef unsigned int result_type;
The type is a synonym for unsigned int.
ranlux_base_01typedef subtract_with_carry_01<float, 24, 10, 24> ranlux_base_01;
The type is a synonym for a specialization of the template subtract_with_carry_01.
ranlux24typedef discard_block_engine<ranlux_24_base, 223, 23>
ranlux24; [added with C++11]
The type is a synonym for a specialization of the template discard_block_engine
with a specialization of the template subtract_with_carry_engine.
ranlux24_basetypedef subtract_with_carry_engine<ui-type, 24, 10, 24>
ranlux24_base; [added with C++11]
The type is a synonym for a specialization of the template
subtract_with_carry_engine.
ranlux3typedef discard_block<subtract_with_carry< ui-type, 1 << 24, 10, 24>
223, 24> ranlux3;
The type is a synonym for a specialization of the template discard_block
with a specialization of the template subtract_with_carry.
ranlux3_01typedef discard_block<ranlux_base_01, 223, 24> ranlux3_01;
The type is a synonym for a specialization of the template discard_block
with a specialization of the template subtract_with_carry_01.
ranlux4typedef discard_block<subtract_with_carry< ui-type, 1 << 24, 10, 24>,
389, 24> ranlux4;
The type is a synonym for a specialization of the template discard_block
with a specialization of the template subtract_with_carry.
ranlux4_01typedef discard_block<ranlux_base_01, 389, 24> ranlux4_01;
The type is a synonym for a specialization of the template discard_block
with a specialization of the template subtract_with_carry_01.
ranlux48typedef discard_block_engine<ranlux_48_base, 389, 11>
ranlux48; [added with C++11]
The type is a synonym for a specialization of the template discard_block_engine
with a specialization of the template subtract_with_carry_engine.
ranlux48_basetypedef subtract_with_carry_engine<ui-type, 48, 5, 12>
ranlux48_base; [added with C++11]
The type is a synonym for a specialization of the template
subtract_with_carry_engine.
ranlux64_base_01typedef subtract_with_carry_01<double, 48, 10, 24> ranlux64_base_01;
The type is a synonym for a specialization of the template subtract_with_carry_01.
seed_seqclass seed_seq { [added with C++11]
public:
typedef uint_least32_t result_type;
seed_seq();
template<class Ty>
seed_seq(initializer_list<Ty> init);
template<class InIt>
seed_seq(InIt first, InIt last);
template<class RanIt>
void generate(RanIt first, RanIt last,
size_t inbits = numeric_limits<typename iterator_traits<
InIt>::value_type>::digits) const;
size_t size() const;
template<class OutIt>
void param(OutIt dest) const;
private:
vector<result_type> vec; // exposition only
};
The class stores a vector of unsigned integer values that can supply a randomized seed for a random-number engine.
seed_seq::generatetemplate<class RanIt>
void generate(RanIt first, RanIt last) const;
The template function initializes the elements of the sequence
[first, last) (if the sequence is non-empty) as follows:
const size_t s = vec.size();
const size_t n = last - first;
const size_t t = 623 <= n ? 11 : 68 <= n ? 7
: 39 <= n ? 5 : 7 <= n ? 3 : (n - 1) / 2;
const size_t p = (n - t) / 2;
const size_t q = p + t;
const size_t m = n <= s ? s + 1 : n;
size_t k;
for (k = 0; k < n; ++k)
first[k] = 0x8b8b8b8b;
for (k = 0; k < m; ++k)
{ // scramble and add any vector contribution
result_type r1 = 1664525
* xor27(first[k % n] ^ first[(k + p) % n] ^ first[(k - 1) % n]);
result_type r2 = r1
+ (k == 0 ? s : k <= s ? k % n + vec[k - 1] : k % n);
first[(k + p) % n] += r1;
first[(k + q) % n] += r2;
first[k] = r2;
}
for (; k < m + n; ++k)
{ // rescramble
result_type r3 = 1566083941
* xor27(first[k % n] + first[(k + p) % n] + first[(k - 1) % n]);
result_type r4 = r3 - k % n;
first[(k + p) % n] ^= r3;
first[(k + q) % n] ^= r4;
first[k] = r4;
}
The function xor27 is defined as:
result_type xor27(result_type val) const
{ // shift and merge
return (val ^ (val >> 27));
}
seed_seq::paramtemplate<class OutIt>
void param(OutIt dest) const;
The template function executes copy(vec.begin(), vec.end(), dest).
seed_seq::result_typetypedef uint_least32_t result_type;
The type is a synonym for uint_least32_t.
seed_seq::seed_seqseed_seq();
template<class Ty>
seed_seq(initializer_list<Ty> init);
template<class InIt>
seed_seq(InIt first, InIt last,
size_t inbits = numeric_limits<typename iterator_traits<
InIt>::value_type>::digits);
The first constructor initializes vec to an empty vector.
The second constructor initializes vec with a sequence of
elements in [init.begin(), init.end()), each reduced modulo 2^32.
The third constructor initializes vec with a sequence of
elements in [first, last), each reduced modulo 2^32.
shuffle_order_enginetemplate<class Engine,
size_t K>
class shuffle_order_engine { [added with C++11]
public:
typedef Engine base_type;
typedef typename base_type::result_type result_type;
static constexpr size_t table_size = K;
shuffle_order_engine();
explicit shuffle_order_engine(const base_type& eng);
explicit shuffle_order_engine(result_type x0);
template<class Seed_seq>
explicit shuffle_order_engine(Seed_seq& seq);
void seed();
void seed(result_type x0);
template<class Seed_seq>
void seed(Seed_seq& seq);
const base_type& base() const noexcept;
static constexpr result_type min();
static constexpr result_type max();
result_type operator()();
void discard(unsigned long long count);
private:
Engine stored_eng; // exposition only
result_type stored_arr[K]; // exposition only
result_type stored_y; // exposition only
};
The template class describes a compound engine
that produces values by reordering the values
returned by its base engine. Each constructor fills the array stored_arr
with K values returned by the base engine. It then stores in
stored_y an additional value returned by the base engine.
Each element of the generated sequence is then obtained from stored_y,
after which:
J is computed as K * (stored_y - min())
/ (max() - min() + 1).stored_y is replaced by stored_arr[J].stored_arr[j] is replaced by stored_eng().The engine's state is the state of stored_eng,
followed by the K elements of stored_arr, followed by
stored_y.
The value of the template argument K must be greater than zero.
shuffle_order_engine::baseconst base_type& base() const noexcept;
The member function returns a reference to the underlying engine object.
shuffle_order_engine::base_typetypedef Engine base_type;
The type is a synonym for the type of the underlying engine object.
shuffle_order_engine::discardvoid discard(unsigned long long count);
The member function effectively calls (*this)() count times.
shuffle_order_engine::maxstatic constexpr result_type max();
The static member function returns Engine::max().
shuffle_order_engine::minstatic constexpr result_type min();
The static member function returns Engine::min().
shuffle_order_engine::operator()result_type operator()();
The member function returns the next value in the sequence.
shuffle_order_engine::result_typetypedef typename base_type::result_type result_type;
The type is a synonym for base_type::result_type.
shuffle_order_engine::seedvoid seed(); void seed(result_type x0); void seed(Seed_seq& seq);
The first seed function
calls stored_eng.seed().
The second seed function calls stored_eng.seed(x0).
The third seed function calls stored_eng.seed(seq).
Unless Seed_seq is not convertible to result_type,
the third function does not participate in overload resolution.
shuffle_order_engine::shuffle_order_engineshuffle_order_engine();
explicit shuffle_order_engine(const base_type& eng);
explicit shuffle_order_engine(result_type x0);
template<class Seed_seq>
explicit shuffle_order_engine(Seed_seq& seq);
The first constructor constructs a shuffle_order_engine object with a default-initialized
engine. The second contructor constructs a shuffle_order_engine object with a copy of an
engine object. The third constructor constructs a shuffle_order_engine object with its engine
initialized by stored_engine(x0).
The fourth constructor constructs a
shuffle_order_engine object with its engine initialized by
stored_engine(seq).
Unless Seed_seq is not convertible to result_type,
the fourth constructor does not participate in overload resolution.
shuffle_order_engine::table_sizestatic constexpr size_t table_size = K;
The static const variable has the same value as the template parmaeter K.
student_t_distributiontemplate<class RealType = double>
class student_t_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit student_t_distribution(RealType n0 = 1);
explicit student_t_distribution(const param_type& par0);
RealType n() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
RealType stored_n; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with a Student T distribution.
student_t_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
student_t_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
student_t_distribution::nRealType n() const;
The member function returns the stored value stored_n.
student_t_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
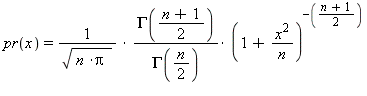
The second member function behaves the same, except that it uses the parameters
stored in par0.
student_t_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
student_t_distribution::param_typestruct param_type {
typedef student_t_distribution<RealType> distribution_type;
param_type(RealType n0 = 1);
RealType n() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
student_t_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
student_t_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
student_t_distribution::student_t_distributionstudent_t_distribution(RealType n0 = 1); explicit student_t_distribution(const param_type& par0);
Precondition: 0.0 < n0
The first constructor constructs an object whose stored value stored_n
holds the value n0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
subtract_with_carrytemplate<class IntType,
IntType M, int S, int R>
class subtract_with_carry {
public:
typedef IntType result_type;
static constexpr IntType modulus = M;
static constexpr int short_lag = S;
static constexpr int long_lag = R;
subtract_with_carry();
explicit subtract_with_carry(IntType x0);
template<class Gen>
subtract_with_carry(Gen& gen);
void seed(IntType x0 = 19780503UL);
template<class Gen>
void seed(Gen& gen);
result_type min() const;
result_type max() const;
result_type operator()();
};
The template class describes a simple engine
that produces values of a user-specified integral type using the
recurrence relation
x(i) = (x(i - R) - x(i - S) - cy(i - 1)) mod M, where
cy(i) has the value 1 if
x(i - S) - x(i - R) - cy(i - 1) < 0,
otherwise 0.
The engine's state is a carry indicator plus
R values. These values consist of the
last R values returned if operator() has been called at least
R times, otherwise the N values that have been returned and
the last R - N values of the
seed.
The template argument IntType must be
large enough to hold values up to M - 1. The values of the template arguments
S and R must be greater than 0 and S must be
less than R.
subtract_with_carry::long_lagstatic constexpr int long_lag = R;
The static const variable holds the value of the template argument R.
subtract_with_carry::maxresult_type max() const;
The member function returns M - 1.
subtract_with_carry::minresult_type min() const;
The member function returns zero.
subtract_with_carry::modulusstatic constexpr IntType modulus = M;
The static const variable holds the value of the template argument M.
subtract_with_carry::operator()result_type operator()();
The member function generates the next value in the pseudo-random sequence by applying the recurrence relation to the stored historical values, stores the generated value, and returns it.
subtract_with_carry::result_typetypedef IntType result_type;
The type is a synonym for IntType.
subtract_with_carry::seedvoid seed(unsigned long x0 = 19780503UL);
template<class Gen>
void seed(Gen& gen);
Precondition: 0 < x0
The first seed function
generates long_lag historical values
from the values of type unsigned long returned by successive invocations of
gen. Each historical value is gen() % modulus.
The second seed function effectively executes the following code:
linear_congruential<unsigned long, 40014, 0, 2147483563> gen(x0);
seed(gen);
subtract_with_carry::short_lagstatic constexpr int short_lag = S;
The static const variable holds the value of the template argument S.
subtract_with_carry::subtract_with_carrysubtract_with_carry();
explicit subtract_with_carry(unsigned long x0);
template<class Gen>
subtract_with_carry(Gen& gen);
The first constructor constructs an object and initializes it by calling seed().
The second constructor constructs an object and initializes it by calling seed(x0).
The third constructor constructs an object and initializes it by
calling seed(gen).
subtract_with_carry_enginetemplate<class UIntType,
int W, int S, int R>
class subtract_with_carry_engine { [added with C++11]
public:
typedef UIntType result_type;
static constexpr int word_size = W;
static constexpr int short_lag = S;
static constexpr int long_lag = R;
static constexpr UIntType default_seed = 19780503U;
explicit subtract_with_carry_engine(UIntType x0 = default_seed);
template<class Seed_seq>
explicit subtract_with_carry_engine(Seed_seq& seq);
void seed(UIntType x0 = default_seed);
template<class Seed_seq>
void seed(Seed_seq& seq);
static constexpr result_type min();
static constexpr result_type max();
result_type operator()();
void discard(unsigned long long count)();
};
The template class describes a simple engine
that produces values of a user-specified unsigned integral type using the
recurrence relation
x(i) = (x(i - R) - x(i - S) - cy(i - 1)) mod M, where
cy(i) has the value 1 if
x(i - S) - x(i - R) - cy(i - 1) < 0,
otherwise 0, and M has the value 2W.
(Note that the template parameter W here replaces the template
parameter M for
subtract_with_carry.)
The engine's state is a carry indicator plus
R values. These values consist of the
last R values returned if operator() has been called at least
R times, otherwise the N values that have been returned and
the last R - N values of the
seed.
The template argument UIntType must be
large enough to hold values up to M - 1. The values of the template arguments
S and R must be greater than 0 and S must be
less than R.
subtract_with_carry_engine::default_seedstatic constexpr UIntType default_seed = 19780503U;
The static const variable holds the default seed value 19780503U.
subtract_with_carry_engine::discardvoid discard(unsigned long long count);
The member function effectively calls (*this)() count times.
subtract_with_carry_engine::long_lagstatic constexpr int long_lag = R;
The static const variable holds the value of the template argument R.
subtract_with_carry_engine::maxstatic constexpr result_type max();
The member function returns M - 1.
subtract_with_carry_engine::minstatic constexpr result_type min();
The member function returns zero.
subtract_with_carry_engine::operator()result_type operator()();
The member function generates the next value in the pseudo-random sequence by applying the recurrence relation to the stored historical values, stores the generated value, and returns it.
subtract_with_carry_engine::result_typetypedef UIntType result_type;
The type is a synonym for UIntType.
subtract_with_carry_engine::seedvoid seed(UIntType x0 = default_seed);
template<class Seed_seq>
void seed(Seed_seq& seq);
Precondition: 0 < x0
The first seed function
effectively constructs the engine gen:
linear_congruential_engine<UIntType, 40014, 0, 2147483563>
gen(x0 == 0 ? default_seed: x0);
It then sets the R historical values beginning with h[0] to
the values produced by calling gen().
The second seed function sets these historical values as follows:
k is the number of unsigned long integers needed to supply
all the bits in a UIntType integer (at least 1).a is an array of R * k elements of type UIntType.a is initialized by calling
seq.generate(&a[0], &a[R * k]).h[i] is composed by packing the k
elements beginning at a[i * k], which supplies the lowest-order bits.h[i] is reduced modulo M.Unless Seed_seq is not convertible to result_type,
the second function does not participate in overload resolution.
In either case, the stored carry is h[R - 1] == 0.
subtract_with_carry_engine::short_lagstatic constexpr int short_lag = S;
The static const variable holds the value of the template argument S.
subtract_with_carry_engine::subtract_with_carry_engineexplicit subtract_with_carry_engine(UIntType x0 = default_seed);
template<class Seed_seq>
subtract_with_carry_engine(Seed_seq& seq);
The first constructor constructs an object and initializes it by calling seed(x0).
The second constructor constructs an object and initializes it by
calling seed(seq).
Unless Seed_seq is not convertible to result_type,
the second constructor does not participate in overload resolution.
subtract_with_carry_engine::word_sizestatic constexpr int word_size = W;
The static const variable holds the value of the template argument W.
subtract_with_carry_01template<class RealType,
int W, int S, int R>
class subtract_with_carry_01 {
public:
typedef RealType result_type;
static constexpr int word_size = W;
static constexpr int short_lag = S;
static constexpr int long_lag = R;
subtract_with_carry_01();
explicit subtract_with_carry_01(unsigned long x0);
template<class Gen>
subtract_with_carry_01(Gen& gen);
void seed(unsigned long x0 = 19780503UL);
template<class Gen>
void seed(Gen& gen);
result_type min() const;
result_type max() const;
result_type operator()();
};
The template class describes a simple engine
that produces values of a user-specified floating-point type using the
recurrence relation
x(i) = (x(i - R) - x(i - S) - cy(i - 1)) mod 1, where
cy(i) has the value 2-W if
x(i - S) - x(i - R) - cy(i - 1) < 0,
otherwise 0. The engine's state is the
last R values returned if operator() has been called at least
R times, otherwise the M values that have been returned and
the last R - M values of the
seed.
The template argument RealType must be
large enough to hold values with W fraction bits. The values of the template arguments
S and R must be greater than 0 and S must be
less than R.
subtract_with_carry_01::long_lagstatic constexpr int long_lag = R;
The static const variable holds the value of the template argument R.
subtract_with_carry_01::maxresult_type max() const;
The member function returns the largest value in the generated sequence.
subtract_with_carry_01::minresult_type min() const;
The member function returns zero.
subtract_with_carry_01::operator()result_type operator()();
The member function generates the next value in the pseudo-random sequence by applying the recurrence relation to the stored historical values, stores the generated value, and returns it.
subtract_with_carry01::result_typetypedef RealType result_type;
The type is a synonym for RealType.
subtract_with_carry_01::seedtemplate<class Gen>
void seed(Gen& gen);
void seed(unsigned long x0 = 19780503UL);
Precondition: 0 < x0
The first seed function
generates long_lag historical values
from the values of type unsigned long returned by successive invocations of
gen. Each historical value is generated
by concatenating the low 32 bits from each of long_lag * (word_size + 31) / 32
values from the initialization sequence; the resulting value is then divided by
2.0word_size and the integral part discarded. Thus, each historical value
is a floating-point value greater than or equal to 0.0 and less than 1.0, with
word_size significant bits.
The second seed function effectively executes the following code:
linear_congruential<unsigned long, 40014, 0, 2147483563> gen(x0);
seed(gen);
subtract_with_carry_01::short_lagstatic constexpr int short_lag = S;
The static const variable holds the value of the template argument S.
subtract_with_carry_01::subtract_with_carry_01subtract_with_carry_01();
explicit subtract_with_carry_01(IntType x0);
template<class In>
subtract_with_carry_01(InIt& first, InIt last);
The first constructor constructs an object and initializes it by calling seed().
The second constructor constructs an object and initializes it by calling seed(x0).
The third constructor constructs an object and initializes it by
calling seed(first, last).
subtract_with_carry_01::word_sizestatic constexpr int word_size = W;
The static const variable holds the value of the template argument W.
uniform_inttemplate<class IntType = int>
class uniform_int {
public:
typedef IntType input_type; [removed with C++11]
typedef IntType result_type;
explicit uniform_int(result_type min0 = 0,
result_type max0 = 9);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng, result_type n);
private:
result_type stored_min; // exposition only
result_type stored_max; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type with a uniform distribution.
uniform_int::input_typetypedef IntType input_type; [removed with C++11]
The type is a synonym for IntType.
uniform_int::maxresult_type max() const;
The member function returns stored_max.
uniform_int::minresult_type min() const;
The member function returns stored_min.
uniform_int::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng, result_type n);
The first member operator uses the engine eng
as a source of uniformly distributed integral values and returns integral values with
each value i in the closed range [min(), max()] occurring
with equal probability and values outside that range occurring with probability 0.
The second member function uses the engine eng
as a source of uniformly distributed integral values and returns integral values with
each value i in the half-open range [0, n) occurring
with equal probability and values outside that range occurring with probability 0.
uniform_int::resetvoid reset();
The member function discards any stored values in the generated sequence.
uniform_int::result_typetypedef IntType result_type;
The type is a synonym for IntType.
uniform_int::uniform_intexplicit uniform_int(result_type min0 = 0, result_type max0 = 9);
Precondition: min0 < max0
The constructor constructs an object whose stored value stored_min
holds the value min0 and whose stored value stored_max
holds the value max0.
uniform_int_distributiontemplate<class IntType = int>
class uniform_int_distribution { [added with C++11]
public:
typedef IntType result_type;
struct param_type;
explicit uniform_int_distribution(result_type min0 = 0,
result_type max0 = numeric_limits<IntType>::max());
explicit uniform_int_distribution(const param_type& par0);
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_min; // exposition only
result_type stored_max; // exposition only
};
The template class describes a distribution that produces values of a user-specified integral type with a uniform distribution.
uniform_int_distribution::aresult_type a() const;
The member function returns the parameter stored_max.
uniform_int_distribution::bresult_type b() const;
The member function returns the parameter stored_min.
uniform_int_distribution::maxresult_type max() const;
The member function returns stored_max.
uniform_int_distribution::minresult_type min() const;
The member function returns stored_min.
uniform_int_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed integral values and returns integral values with
each value i in the closed range [min(), max()] occurring
with equal probability and values outside that range occurring with probability 0.
The second member function behaves the same, except that it uses the parameters
stored in par0.
uniform_int_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
uniform_int_distribution::param_typestruct param_type {
typedef uniform_int_distribution<IntType> distribution_type;
param_type(result_type a0 = 0,
result_type b0 = numeric_limits<IntType>::max());
result_type a() const;
result_type b() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
uniform_int_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
uniform_int_distribution::result_typetypedef IntType result_type;
The type is a synonym for IntType.
uniform_int_distribution::uniform_int_distributionexplicit uniform_int_distribution(result_type min0 = 0,
result_type max0 = numeric_limits<IntType>::max());
explicit uniform_int_distribution(const param_type& par0);
Precondition: min0 < max0
The first constructor constructs an object whose stored value stored_min
holds the value min0 and whose stored value stored_max
holds the value max0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
uniform_realtemplate<class RealType = double>
class uniform_real {
public:
typedef RealType input_type; [removed with C++11]
typedef RealType result_type;
explicit uniform_real(result_type min0 = result_type(0),
result_type max0 = result_type(1));
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
private:
result_type stored_min; // exposition only
result_type stored_max; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type with a uniform distribution.
uniform_real::input_typetypedef RealType input_type; [removed with C++11]
The type is a synonym for RealType.
uniform_real::maxresult_type max() const;
The member function returns stored_max.
uniform_real::minresult_type min() const;
The member function returns stored_min.
uniform_real::operator()template<class Engine>
result_type operator()(Engine& eng);
The member function uses the engine eng
as a source of uniformly distributed floating-point values and returns floating-point values with
each value x in the half-open range [min(), max()) occurring
with equal probability, and values outside that range occurring with probability 0.
uniform_real::resetvoid reset();
The member function discards any stored values in the generated sequence.
uniform_real::result_typetypedef RealType result_type;
The type is a synonym for RealType.
uniform_real::uniform_realexplicit uniform_real(result_type min0 = result_type(0),
result_type max0 = result_type(1));
Precondition: min0 < max0
The constructor constructs an object whose stored value stored_min
holds the value min0 and whose stored value stored_max
holds the value max0.
uniform_real_distributiontemplate<class RealType = double>
class uniform_real_distribution {
public:
typedef RealType result_type;
struct param_type;
explicit uniform_real_distribution(result_type min0 = result_type(0.0),
result_type max0 = result_type(1.0));
explicit uniform_real_distribution(const param_type& par0);
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_min; // exposition only
result_type stored_max; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type with a uniform distribution.
uniform_real_distribution::aresult_type a() const;
The member function returns the parameter stored_max.
uniform_real_distribution::bresult_type b() const;
The member function returns the parameter stored_min.
uniform_real_distribution::maxresult_type max() const;
The member function returns stored_max.
uniform_real_distribution::minresult_type min() const;
The member function returns stored_min.
uniform_real_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The member function uses the engine eng
as a source of uniformly distributed floating-point values and returns floating-point values with
each value x in the half-open range [min(), max()) occurring
with equal probability, and values outside that range occurring with probability 0.
The second member function behaves the same, except that it uses the parameters
stored in par0.
uniform_real_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
uniform_real_distribution::param_typestruct param_type {
typedef uniform_real_distribution<RealType> distribution_type;
param_type(result_type a0 = result_type(0.0),
result_type b0 = result_type(1.0));
result_type a() const;
result_type b() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
uniform_real_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
uniform_real_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
uniform_real_distribution::uniform_real_distributionexplicit uniform_real_distribution(result_type min0 = result_type(0.0),
result_type max0 = result_type(1.0));
explicit uniform_real_distribution(const param_type& par0);
Precondition: min0 < max0
The first constructor constructs an object whose stored value stored_min
holds the value min0 and whose stored value stored_max
holds the value max0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
variate_generatortemplate<class Engine, class Dist>
class variate_generator { [removed with C++11]
public:
typedef Engine engine_type;
typedef engine-return-type engine_value_type;
typedef Dist distribution_type;
typedef typename Dist::result_type result_type;
variate_generator(engine_type eng0, distribution_type dist0);
result_type operator()();
template<class T>
result_type operator()(T value);
engine_value_type& engine();
const engine_value_type& engine() const;
distribution_type& distribution();
const distribution_type& distribution() const;
result_type min() const;
result_type max() const;
private:
Engine eng; // exposition only
Dist dist; // exposition only
};
The template class describes an object that holds an
engine and a
distribution and produces values by
passing the wrapped engine object to the
distribution object's operator().
The template argument Engine can be a type Eng,
Eng*, or Eng&, where Eng is an
engine. The type Eng is
the underlying engine type.
The corresponding object of type Eng is the
the underlying engine object.
The template uses a wrapped engine to match
the type of the values produced by the engine object to the type of
values required by the distribution object. The wrapped engine's
operator() returns values of type Dist::input_type,
generated as follows:
Engine::result_type and Dist::input_type are both
integral types it returns eng(),
converted to type Dist::input_type.Engine::result_type and Dist::input_type are both
floating-point types it returns (eng() - eng.min()) / (eng.max() - eng.min()),
converted to type Dist::input_type.Engine::result_type is an integral type and Dist::input_type
is a floating-point type it returns (eng() - eng.min()) / (eng.max() - eng.min() + 1),
converted to type Dist::input_type.Engine::result_type is a floating-point type and Dist::input_type
is an integral type it returns
((eng() - eng.min()) / (eng.max() - eng.min()) * numeric_limits<Dist::input_type>::max(),
converted to type Dist::input_type.variate_generator::distributiondistribution_type& distribution(); const distribution_type& distribution() const;
The member functions return a reference to the stored distribution object dist.
variate_generator::distribution_typetypedef Dist distribution_type;
The type is a synonym for the template parameter Dist.
variate_generator::engineengine_value_type engine(); const engine_value_type& engine() const;
The member functions return a reference to the underlying engine object.
variate_generator::engine_typetypedef Engine engine_type;
The type is a synonym for the template parameter Engine.
variate_generator::engine_value_typetypedef engine-value-type engine_value_type;
The type is a synonym for the type of values returned by the underlying engine type.
variate_generator::maxresult_type max() const;
The member function returns dist.max().
variate_generator::minresult_type min() const;
The member function returns dist.min().
variate_generator::operator()result_type operator()();
template<class T>
result_type operator()(T value);
The first member operator returns dist(wr_eng), where wr_eng
is the object's wrapped engine.
The second member function returns dist(wr_eng, value), where wr_eng
is the object's wrapped engine.
variate_generator::result_typetypedef typename Dist::result_type result_type;
The type is a synonym for Dist::result_type.
variate_generator::variate_generatorvariate_generator(engine_type eng0, distribution_type dist0);
The constructor constructs an object whose stored value eng
holds eng0 and whose stored value dist holds dist0.
weibull_distributiontemplate<class RealType = double>
class weibull_distribution { [added with C++11]
public:
typedef RealType result_type;
struct param_type;
explicit weibull_distribution(result_type a0 = result_type(1.0),
result_type b0 = result_type(1.0));
explicit weibull_distribution(const param_type& par0);
result_type a() const;
result_type b() const;
param_type param() const;
void param(const param_type& par0);
result_type min() const;
result_type max() const;
void reset();
template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
private:
result_type stored_a; // exposition only
result_type stored_b; // exposition only
};
The template class describes a distribution that produces values of a user-specified floating-point type distributed with a Weibull distribution.
weibull_distribution::aresult_type a() const;
The member function returns the stored value stored_a.
weibull_distribution::bresult_type b() const;
The member function returns the stored value stored_b.
weibull_distribution::maxresult_type max() const;
The member function returns the largest value returnable by
operator().
weibull_distribution::minresult_type min() const;
The member function returns the smallest value returnable by
operator().
weibull_distribution::operator()template<class Engine>
result_type operator()(Engine& eng);
template<class Engine>
result_type operator()(Engine& eng,
const param_type& par0);
The first member operator uses the engine eng
as a source of uniformly distributed random integral values and returns
floating-point values with each value x occurring with probability:
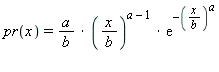
The second member function behaves the same, except that it uses the parameters
stored in par0.
weibull_distribution::paramparam_type param() const; void param(const param_type& par0);
The first member function returns and object that stores
all the parameters of the distribution. The second member function
initializes all the parameters from par0.
weibull_distribution::param_typestruct param_type {
typedef weibull_distribution<RealType> distribution_type;
param_type(result_type a0 = result_type(1.0),
result_type b0 = result_type(1.0));
result_type a() const;
result_type b() const;
.....
bool operator==(const param_type& right) const;
bool operator!=(const param_type& right) const;
};
The type is a class that can store all the parameters of the distribution.
weibull_distribution::resetvoid reset();
The member function discards any stored values in the generated sequence.
weibull_distribution::result_typetypedef RealType result_type;
The type is a synonym for RealType.
weibull_distribution::weibull_distributionweibull_distribution(result_type a0 = result_type(1.0),
result_type b0 = result_type(1.0));
explicit weibull_distribution(const param_type& par0);
Precondition: 0.0 < a0 && 0.0 < b0
The first constructor constructs an object whose stored value stored_a
holds the value a0 and whose stored value stored_b holds
the value b0.
The second constructor constructs an object whose stored parameters
are initialized from par0.
xor_combinetemplate<class Engine1, int S1,
class Engine2, int S2>
class xor_combine { [removed with C++11]
public:
typedef Engine1 base1_type;
typedef Engine2 base2_type;
typedef T1 result_type;
static constexpr int shift1 = S1;
static constexpr int shift2 = S2;
xor_combine();
xor_combine(result_type x0);
xor_combine(const base1_type& eng1, const base2_type& eng2);
template<class Gen>
xor_combine(Gen& gen);
void seed();
template<class Gen>
void seed(Gen& gen);
const base1_type& base1() const;
const base2_type& base2() const;
result_type min() const;
result_type max() const;
result_type operator()();
private:
base1_type stored_eng1; // exposition only
base2_type stored_eng2; // exposition only
};
The template class describes a compound engine
that produces values by combining values produced by two engines. The engine's
state is the state of stored_eng1
followed by the state of stored_eng2.
xor_combine::base1const base1_type& base1() const;
The member function returns a reference to the stored value stored_eng1.
xor_combine::base1_typetypedef Engine1 base1_type;
The type is a synonym for the template parameter Engine1.
xor_combine::base2const base2_type& base2() const;
The member function returns a reference to the stored value stored_eng2.
xor_combine::base2_typetypedef Engine1 base2_type;
The type is a synonym for the template parameter Engine2.
xor_combine::maxresult_type max() const;
The member function returns the largest value in the generated sequence.
xor_combine::minresult_type min() const;
The member function returns the smallest value in the generated sequence.
operator()result_type operator()();
The member operator returns (stored_eng1() << shift1) ^ (stored_eng2() << shift2).
xor_combine::result_typetypedef T1 result_type;
The type is a synonym for the unnamed type T1,
which is either Engine1::result_type
or Engine2::result_type, whichever has the larger range of
values.
xor_combine::seedvoid seed();
template<class Gen>
void seed(Gen& gen);
The first seed function
calls stored_eng1.seed() and then calls
stored_eng2.seed(). The second seed function calls
stored_eng1.seed(gen) and then calls
stored_eng2.seed(gen).
xor_combine::shift1static constexpr int shift1 = S1;
The static const variable holds the value of the template argument S1.
xor_combine::shift2static constexpr int shift2 = S2;
The static const variable holds the value of the template argument S2.
xor_combine::xor_combinexor_combine();
xor_combine(result_type x0);
xor_combine(const base1_type& eng1, const base2_type& eng2);
template<class Gen>
xor_combine(Gen& gen);
The first constructor constructs an object with stored values stored_eng1
and stored_eng2 constructed with their respective default constructors.
The second constructor constructs an object with stored values stored_eng1
and stored_eng2 constructed with x0 and x0 + 1,
respectively.
The third constructor constructs an object whose stored value stored_eng1
holds a copy of eng1 and whose stored value stored_eng2
holds a copy of eng2.
The fourth constructor constructs an object and calls seed(gen).
See also the Table of Contents and the Index.
Copyright © 1992-2013 by Dinkumware, Ltd. All rights reserved.